
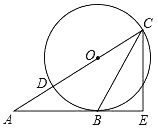
【题目】如图,已知△ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE⊥AB,交AB的延长线于点E.
(1)求证:CB平分∠ACE;
(2)若BE=![]() ,CE=2,求⊙O的半径.
,CE=2,求⊙O的半径.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)如图,连接OB,如图,利用切线的性质得到OB⊥AB,则OB∥CE,根据平行线的性质得∠1=∠3,加上∠1=∠2,所以∠2=∠3;
(2)如图,连接BD,先利用勾股定理计算出BC=![]() ,再证明△DBC∽△BEC,然后利用相似比求出CD的长,从而得到⊙O的半径.
,再证明△DBC∽△BEC,然后利用相似比求出CD的长,从而得到⊙O的半径.
(1)如图,连接OB,
∵AB是⊙O的切线,
∴OB⊥AB,
∵CE⊥AB,
∴OB∥CE,
∴∠1=∠3,
∵OB=OC,
∴∠1=∠2,
∴∠2=∠3,
∴CB平分∠ACE;
(2)如图,连接BD,
∵CE⊥AB,
∴∠E=90°,
∴BC=![]() ,
,
∵CD是⊙O的直径,
∴∠DBC=90°,
∴∠E=∠DBC,
由(1)得∠2=∠3,
∴△DBC∽△BEC,
∴CD:BC=BC:CE,
∴CD= ,
,
∴⊙O的半径为![]() .
.



科目:初中数学 来源: 题型:
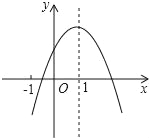
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列6个结论:
①abc<0;
②b<a﹣c;
③4a+2b+c>0;
④2c<3b;
⑤a+b<m(am+b),(m≠1的实数)
⑥2a+b+c>0,其中正确的结论的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 外接圆的圆心,过点
外接圆的圆心,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 的切线,交
的切线,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
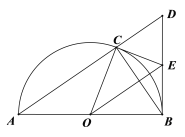
(1)求证:![]() ;
;
(2)填空:①当![]() 的度数为_________时,四边形
的度数为_________时,四边形![]() 为平行四边形;
为平行四边形;
②当![]() 时,
时,![]() 的值为____________.
的值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
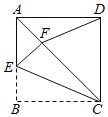
【题目】如图,在正方形ABCD的边AB上取一点E,连接CE,将△BCE沿CE翻折,点B恰好与对角线AC上的点F重合,连接DF,若BE=2,则△CDF的面积是( )
A.1![]() B.3
B.3![]() C.6
C.6![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】许昌芙蓉湖位于许昌市水系建设总体规划中部,上游接纳清泥河来水,下游为鹿鸣湖等水系供水,承担着承上启下的重要作用,是利用有限的水资源、形成良好的水生态环境打造生态宜居城市的重要部分.某校课外兴趣小组想测量位于芙蓉湖两端的A,B两点之间的距离他沿着与直线AB平行的道路EF行走,走到点C处,测得∠ACF=45°,再向前走300米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为200米,求A,B两点之间的距离(结果保留一位小数)

查看答案和解析>>
科目:初中数学 来源: 题型:
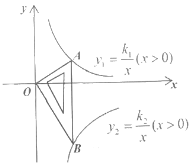
【题目】如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=![]() (x>0)的图象上,顶点B在函数y2=
(x>0)的图象上,顶点B在函数y2= ![]() (x>0)的图象上,∠ABO=30°,则
(x>0)的图象上,∠ABO=30°,则![]() =( )
=( )
A.-3 B.3 C.![]() D.-
D.- ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
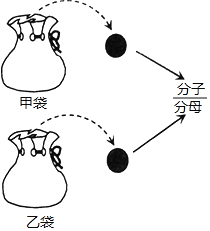
【题目】现有4个质地和大小完全相同的小球,分别标有数字2,3,4,6.将标有2,3的小球放入不透明的甲袋中,标有4,6的小球放入不透明的乙袋中.从甲袋中随机摸出一个球,将球上的数字当作一个分数的分子:再从乙袋中随机摸出一个球,将球上的数字当作这个分数的分母,从而得到一个分数,如图
(1)用列表法(或画树状图)表示所有的可能结果;
(2)小亮说:“得到的分数大于![]() 和小于
和小于![]() 的概率相同”请通过计算说明小亮的说法是否正确.
的概率相同”请通过计算说明小亮的说法是否正确.
查看答案和解析>>
科目:初中数学 来源: 题型:
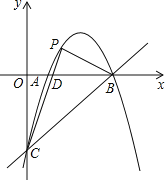
【题目】如图,抛物线y=ax2+5x+c交x轴于A,B两点,交y轴于点C,直线y=x﹣4经过点B,C.P是直线BC上方抛物线上一动点,直线PC交x轴于D.
(1)直接写出a,c的值;
(2)当△PBD的面积等于△BDC面积的一半时,求点P的坐标;
(3)当∠PBA=![]() ∠CBP时,直接写出直线BP的解析式.
∠CBP时,直接写出直线BP的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com