
 如图,正方形ABCD的边长为6,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,求证:MF>DC.
如图,正方形ABCD的边长为6,点E是BC上的一点,连接AE并延长交射线DC于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,求证:MF>DC.  期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:填空题
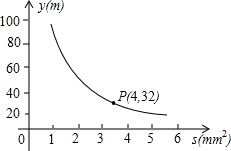 兰州是拉面的故乡,在做拉面的过程中渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示,若工人师傅将面团拉成160根,每根长0.5m时为成品,则此时拉面粗1.6mm2.
兰州是拉面的故乡,在做拉面的过程中渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(m)是面条的粗细(横截面积)S(mm2)的反比例函数,其图象如图所示,若工人师傅将面团拉成160根,每根长0.5m时为成品,则此时拉面粗1.6mm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
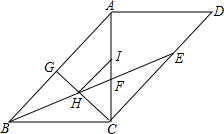 如图,平行四边形ABCD中,对角线AC⊥BC,BE平分∠ABC,交CD于点E,且与AC交于点F.过点C作CG1AB于点G,CG与BE交于点H,点I在线段AC上,且HI∥AB.求证:
如图,平行四边形ABCD中,对角线AC⊥BC,BE平分∠ABC,交CD于点E,且与AC交于点F.过点C作CG1AB于点G,CG与BE交于点H,点I在线段AC上,且HI∥AB.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com