
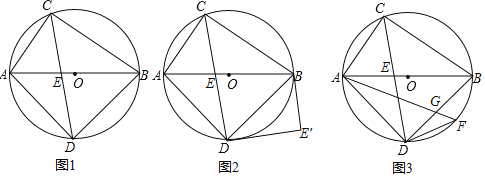
【题目】如图1,AB为⊙O的直径,点C为⊙O上一点,CD平分∠ACB交⊙O于点D,交AB于点E.
(1)求证:△ABD为等腰直角三角形;
(2)如图2,ED绕点D顺时针旋转90°,得到DE′,连接BE′,证明:BE′为⊙O的切线;
(3)如图3,点F为弧BD的中点,连接AF,交BD于点G,若DF=1,求AG的长.
【答案】(1)见解析;(2)见解析;(3)2.
【解析】
(1)由AB是⊙O的直径,根据直径所对的圆周角是直角,即可得∠ADB=90°,又由CD平分∠ACB,根据圆周角定理,可得AD=BD,继而可得△ABD是等腰直角三角形;
(2)证明△ADE≌△BDE',可得∠DAE=∠DBE',则∠OBE'=∠ABD+∠DBE'=90°,结论得证;
(3)取AG的中点H,连结DH,则DH=AH=GH,求出DH=DF=1,则答案可求出.
(1)∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∵CD平分∠ACB,
∴∠ACD=∠DCB,
∴![]() ,
,
∴AD=BD,
∴△ABD是等腰直角三角形.
(2)由旋转的性质得,∠EDE'=90°,DE=DE',
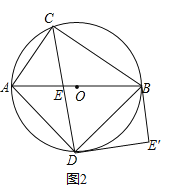
∵∠ADB=90°,
∴∠ADE=∠BDE',
∵AD=BD,
∴△ADE≌△BDE'(SAS),
∴∠DAE=∠DBE',
∵∠EAD=∠DCB=45°,∠ABD=∠DCA=45°,
∴∠OBE'=∠ABD+∠DBE'=90°,
∴BE′为⊙O的切线;
(3)解:∵点F为![]() 的中点,
的中点,
∴∠FAD=![]() ∠DAB=22.5°,
∠DAB=22.5°,
取AG的中点H,连结DH,
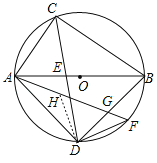
∵∠ADB=90°,
∴DH=AH=GH,
∴∠ADH=∠FAD=22.5°,
∴∠DHF=∠ADH+∠FAD=45°,
∵∠AFD=∠ACD=45°,
∴∠DHF=∠AFD,
∴DH=DF=1,
∴AG=2DH=2.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】从﹣4,﹣3,﹣2,﹣1,0,1,3,4,5这九个数中,随机抽取一个数,记为a,则数a使关于x的不等式组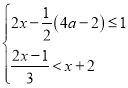 至少有四个整数解,且关于x的分式方程
至少有四个整数解,且关于x的分式方程![]() =1有非负整数解的概率是( )
=1有非负整数解的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,过点(﹣4,0),(0,﹣2).
(1)求抛物线的解析式和顶点坐标;
(2)当﹣4<x<4时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC交AC于点E,AC的反向延长线交⊙O于点F.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若∠C=30°,⊙O的半径为6,求弓形AF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,小王想要了解本小区居民对“广场舞”的看法,于是进行了-次抽样调查,把居民对“广场舞”的看法分为四类:
A.非常赞同; B.赞同但要有时间限制; C.无所谓; D.不赞同.
并将调查结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)①本次被抽查的居民人数是________人;将条形统计图补充完整
②图l中∠α的度数是________度;该小区有3000名居民,请估计对“广场舞”表示赞同(包括A类和B类)的大约有________人.
(2)小王想从甲,乙,丙,丁四位居民中随机选取两位了解具体情况,请用列表或画树状图的方法求出恰好同时选中甲和乙两位居民的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() ,直线
,直线![]() 与y轴交于点A,与双曲线
与y轴交于点A,与双曲线![]() 交于点
交于点![]() .
.
(1)求点B的坐标及k的值;
(2)将直线AB平移,使它与x轴交于点C,与y轴交于点D,若![]() 的面积为6,求直线CD的表达式.
的面积为6,求直线CD的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:
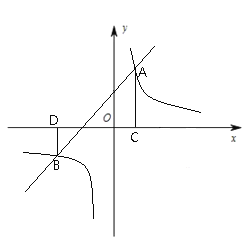
如图所示,在平面直角坐标系中,直线![]() 与反比例函数
与反比例函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() .
.
(1)求![]() ,
,![]() 的值及反比例函数的函数表达式;
的值及反比例函数的函数表达式;
(2)若点![]() 在线段
在线段![]() 上,且
上,且![]() ,请求出此时点
,请求出此时点![]() 的坐标;
的坐标;
(3)小颖在探索中发现:在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是以
是以![]() 为顶角的等腰三角形.请你直接写出点
为顶角的等腰三角形.请你直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com