
【题目】a,b分别是数轴上两个不同的点A,B所表示的有理数,且![]() =5,
=5,![]() =2,A,B两点在数轴上的位置如图所示:
=2,A,B两点在数轴上的位置如图所示:
![]()
(1) 试确定数a,b;
(2) A,B两点相距多少个单位长度?
(3)若C点在数轴上,C点B点的距离是C点到A点距离的![]() ,求C点表示的数;
,求C点表示的数;
【答案】(1)a=-5,b=-2;(2)3个单位长度;(3)![]() 或
或![]()
【解析】
(1)根据绝对值的定义结合由数轴得出a、b的符号即可得;
(2)根据数轴上两点间的距离公式即可得;
(3)设C点表示的数为x,分以下两种情况:点C在A、B之间、点C在点B右侧,利用两点间距离公式列方程求解.
解:(1)∵|a|=5,|b|=2,
∴a=5或-5,b=2或-2,
由数轴可知,a<b<0,
∴a=-5,b=-2;
(2)A、B两点间的距离是-2-(-5)=3;
(3)设C点表示的数为x,
当点C在A、B之间时,根据题意有:x-(-5)=3(-2-x),
解得:![]() ;
;
当点C在点B右侧时,根据题意有:x-(-5)=3[x-(-2)],
解得:![]() .
.
∴C点表示的数为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】观察下列等式:71=7,72=49,73=343,74=2 401,75=16 807,76=117 649,…,那么:71+72+73+…+72 016的末位数字是( )
A. 9B. 7C. 6D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于P.若四边形ABCD的面积是18,则DP的长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在坐标平面内,从点(x,y)移动到点(x+1,y+2)的运动称为一次A类跳马,从点(x,y)移动到点(x+2,y+1)的运动称为一次B类跳马.现在从原点开始出发,连续10次跳马,每次跳马采取A类或B类跳马,最后恰好落在直线![]() 上,则最后落马的坐标是_______.
上,则最后落马的坐标是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
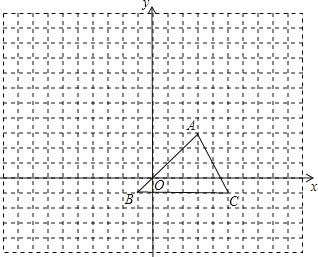
【题目】如图所示的正方形网格,△ABC的顶点在网格上,在建立平面直角坐标系后,点B的坐标是(-1,-1)
(1)把△ABC向左平移10格得到![]() ,画出
,画出![]() ;
;
(2)画出![]() 关于x轴对称的图形
关于x轴对称的图形![]() ;
;
(3)把△ABC绕点C顺时针旋转90°后得到![]() ,画出
,画出![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)=![]() .例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)=
.例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)= ![]() .
.
(1)若F(a)=![]() 且a为100以内的正整数,则a=________;
且a为100以内的正整数,则a=________;
(2)如果m是一个两位数,那么试问F(m)是否存在最大值或最小值?若存在,求出最大(或最小)值以及此时m的取值并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
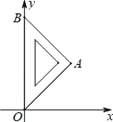
【题目】如图,O为坐标原点,△OAB是等腰直角三角形,∠OAB=90°,点B的坐标为(0,2![]() ),将该三角形沿x轴向右平移得到Rt△O′A′B′,此时点B′的坐标为(2
),将该三角形沿x轴向右平移得到Rt△O′A′B′,此时点B′的坐标为(2![]() ,2
,2![]() ),则线段OA在平移过程中扫过部分的图形面积为( )
),则线段OA在平移过程中扫过部分的图形面积为( )
A. 2B. ![]() C. 4D.
C. 4D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
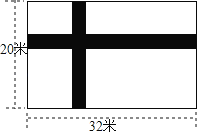
【题目】如图所示,宽为20米,长为32米的长方形地面上,修筑宽度为x米的两条互相垂直的小路,余下的部分作为耕地,如果要在耕地上铺上草皮,选用草皮的价格是每平米a元,
(1)求买草皮至少需要多少元?(用含a,x的式子表示)
(2)计算a=40,x=2时,草皮的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
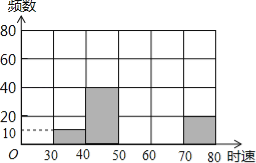
【题目】将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数分布表(未完成):
数据段 | 30~40 | 40~50 | 50~60 | 60~70 | 70~80 | 总计 |
频 数 | 10 | 40 | | | 20 | |
百分比 | 5% | | 40% | | 10% | |
注:30~40为时速大于等于30千米而小于40千米,其他类同.
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果此路段汽车时速超过60千米即为违章,则违章车辆共有多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com