
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,交OD于点F.
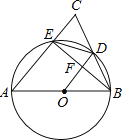
(1)求证:OD⊥BE.
(2)若DE=![]() ,AB=6,求AE的长.
,AB=6,求AE的长.
(3)若△CDE的面积是△OBF面积的![]() ,求线段BC与AC长度之间的等量关系,并说明理由.
,求线段BC与AC长度之间的等量关系,并说明理由.
【答案】(1)证明见解析;(2)4;(3)AC=![]() BC.
BC.
【解析】
(1)连接AD.根据直径所对的圆周角是直角、等腰三角形的性质以及平行线的性质即可证明;
(2)先证△CDE∽△CAB得![]() ,据此求得CE的长,依据AE=AC-CE=AB-CE可得答案;
,据此求得CE的长,依据AE=AC-CE=AB-CE可得答案;
(3)由BD=CD知S△CDE=S△BDE,证△OBF∽△ABE得![]() ,据此知S△ABE=4S△OBF,结合
,据此知S△ABE=4S△OBF,结合![]() 知S△ABE=6S△CDE,S△CAB=8S△CDE,由△CDE∽△CAB知
知S△ABE=6S△CDE,S△CAB=8S△CDE,由△CDE∽△CAB知![]() ,据此得出
,据此得出![]() ,结合BD=CD,AB=AC知
,结合BD=CD,AB=AC知![]() ,从而得出答案.
,从而得出答案.
(1)连接AD,
∵AB是直径,
∴∠AEB=∠ADB=90°,
∵AB=AC,
∴∠CAD=∠BAD,BD=CD,
∴![]() ,
,
∴OD⊥BE;
(2)∵∠AEB=90°,
∴∠BEC=90°,
∵BD=CD,
∴BC=2DE=2![]() ,
,
∵四边形ABDE内接于⊙O,
∴∠BAC+∠BDE=180°,
∵∠CDE+∠BDE=180°,
∴∠CDE=∠BAC,
∵∠C=∠C,
∴△CDE∽△CAB,
∴![]() ,即
,即![]() ,
,
∴CE=2,
∴AE=AC-CE=AB-CE=4;
(3)∵BD=CD,
∴S△CDE=S△BDE,
∵BD=CD,AO=BO,
∴OD∥AC,
∵△OBF∽△ABE,
∴![]() ,
,
∴S△ABE=4S△OBF,
∵![]() ,
,
∴S△ABE=4S△OBF=6S△CDE,
∴S△CAB=S△CDE+S△BDE+S△ABE=8S△CDE,
∵△CDE∽△CAB,
∴![]() ,
,
∴![]() ,
,
∵BD=CD,AB=AC,
∴![]() ,即AC=
,即AC=![]() BC.
BC.


科目:初中数学 来源: 题型:
【题目】国家支持大学生创新办实业,提供小额无息贷款,学生王亮享受国家政策贷款36000元用于代理某品牌服装销售,已知该店代理的品牌服装的进价为每件40元,该品牌服装售量y(件)与销售价x(元/件)之间的关系可用图中的一条线段(实线)来表示.
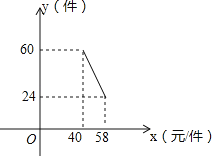
(1)求日销售量y与销售价x之间的函数关系式,并写出x的取值范围;
(2)该品牌服装售价x为多少元时,每天的销售利润W最大,且最大销售利润W为多少?
(3)若该店应支付员工的工资为每人每天82元,每天还应支付其它费用为106元(不包含贷款).现该店只有2名员工,则该店至少需要多少天才能还清所有贷款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() 的图象交于A、B两点,与x轴交于点C;点A在第一象限,点B的坐标为(﹣6,n);E为x轴正半轴上一点,且tan∠AOE=
的图象交于A、B两点,与x轴交于点C;点A在第一象限,点B的坐标为(﹣6,n);E为x轴正半轴上一点,且tan∠AOE=![]() .
.
(1)求点A的坐标;
(2)求一次函数的表达式;
(3)求△AOB的面积.
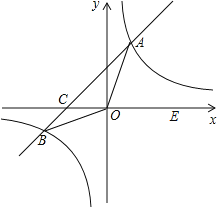
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BC=4,tanB=2,以AB的中点D为圆心,r为半径作⊙D,如果点B在⊙D内,点C在⊙D外,那么r可以取( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区在同一线路上顺次有三个景点A,B,C,甲、乙两名游客从景点A出发,甲步行到景点C;乙花20分钟时间排队后乘观光车先到景点B,在B处停留一段时间后,再步行到景点C.甲、乙两人离景点A的路程s(米)关于时间t(分钟)的函数图像如图所示.
(1)甲的速度是 米/分钟;
(2)当20≤t ≤30时,求乙离景点A的路程s与t的函数表达式;
(3)乙出发后多长时间与甲在途中相遇?
(4)若当甲到达景点C时,乙与景点C的路程为360米,则乙从景点B步行到景点C的速度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
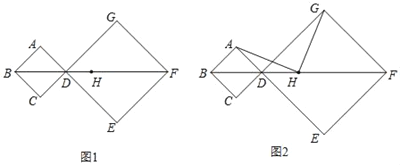
【题目】在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.
(1)如图1,若AB=1,DG=2,求BH的长;
(2)如图2,连接AH,GH.
小宇观察图2,提出猜想:AH=GH,AH⊥GH.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:延长AH交EF于点M,连接AG,GM,要证明结论成立只需证△GAM是等腰直角三角形;
想法2:连接AC,GE分别交BF于点M,N,要证明结论成立只需证△AMH≌△HNG.…
请你参考上面的想法,帮助小宇证明AH=GH,AH⊥GH.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,每人射击10次;根据两人成绩的信息,绘制了统计图,如图所示:
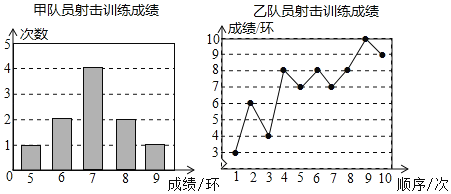
下面有四个推断:
①甲和乙成绩的众数不相同 ②甲和乙成绩的中位数相同
③甲和乙成绩的平均数不相同 ④甲的成绩比乙的成绩稳定
其中合理的是( )
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以![]() 为直径的半圆
为直径的半圆![]() 上有一动点
上有一动点![]() ,点
,点![]() 为弧
为弧![]() 的中点,连接
的中点,连接![]() 、
、![]() 相交于点
相交于点![]() ,延长
,延长![]() 到
到![]() 点,使得
点,使得![]() ,连接
,连接![]() 、
、![]() .
.
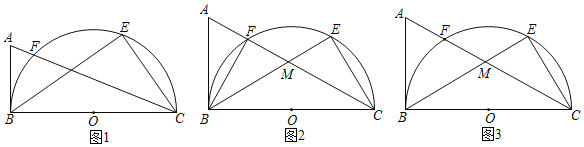
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)如图2,连接![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(3)如图3,若![]() ,
,![]() .求
.求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,抛物线![]() 经过点A(0,-3),B(4,5).
经过点A(0,-3),B(4,5).
(1)求此抛物线表达式及顶点M的坐标;
(2)设点M关于y轴的对称点是N,此抛物线在A,B两点之间的部分记为图象W(包含A,B两点),经过点N的直线l: ![]() 与图象W恰一个有公共点,结合图象,求m的取值范围.
与图象W恰一个有公共点,结合图象,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com