练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．如图，已知AB=CD，BC=AD，∠B=20°，则∠D=（　　）
    A．70°B．60°C．40°D．20°

    分析 首先证明△BAC≌△DCA，再根据全等三角形对应边相等可得∠D=∠B．

    解答 解：∵在△BAC和△DCA中$\left\{\begin{array}{l}{AB=CD}\\{AC=AC}\\{BC=AD}\end{array}\right.$，
    ∴△BAC≌△DCA（SSS），
    ∴∠D=∠B=20°，
    故选：D．

    点评 此题主要考查了全等三角形的判定和性质，关键是掌握全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    8．若实数a，b满足${（a+\sqrt{2}）^2}+\sqrt{b-4}$=0，则$\frac{a^2}{b}$=$\frac{1}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，线段MN表示一段高架道路，线段AB表示高架道路旁的一排居民楼．已知点A到MN的距离为15m，BA的延长线与MN相交于点D，且∠BDN=30°．若汽车沿着从M到N的方向在MN上行驶，方圆39m以内会受到噪音的影响，当其到达点P时，噪音开始影响这一排的居民楼；当其到达点Q时，它与这一排居民楼的距离为39m，求PQ的长度（精确到1m）（参考数据：$\sqrt{3}$≈1.7）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，⊙O为△ABC的外接圆，直线l与⊙O相切与点P，且l∥BC．
    （1）请仅用无刻度的直尺，在⊙O中画出一条弦，使这条弦将△ABC分成面积相等的两部分（保留作图痕迹，不写作法）；
    （2）请写出证明△ABC被所作弦分成的两部分面积相等的思路．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

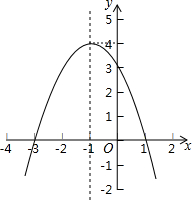    13．已知抛物线y=ax2+bx+c如图所示，请结合图象中所给信息完成以下问题：
    （1）求抛物线的表达式；
    （2）若该抛物线经过一次平移后过原点O，请写出一种平移方法，并写出平移后得到的新抛物线的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．甲经销商库存有1200套A牌服装，每套进价400元，售价500元，一年内可卖完．现市场流行B品牌服装，每套进价300元，售价600元，一年内B品牌服装销售无积压，但一年内只允许经销商一次性订购B品牌服装，因甲经销商无流动资金可用，只有低价转让A品牌服装，用转让来的资金购进B品牌服装，并销售，经与乙经销商协商，甲、乙双方达成转让协议，转让价格y（元/套）与转让数量x（套）之间的函数关系式为y=-$\frac{1}{10}$x+360（100≤x≤1200），若甲经销商转让x套A品牌服装，一年内所获总利润为W（元）．
    （1）求转让后剩余的A品牌服装的销售款Q1（元）与x（套）之间的函数关系式；
    （2）求B品牌服装的销售款Q2（元）与x（套）之间的函数关系式；
    （3）求W（元）与x（套）之间的函数关系式，并求转让多少套时，所获总利润W最大，最大值是多少．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．若A、B、C三点都在直线l上，并且线段AB=3cm，BC=5cm，则线段AC=8或2cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图1，已知数轴上有三点A、B、C，AB=60，点A对应的数是40．

    （1）若BC：AC=4：7，求点C到原点的距离；
    （2）如图2，在（1）的条件下，动点P、Q两点同时从C、A出发向右运动，同时动点R从点A向左运动，已知点P的速度是点R的速度的3倍，点Q的速度是点R的速度2倍少5个单位长度/秒．经过5秒，点P、Q之间的距离与点Q、R之间的距离相等，求动点Q的速度；
    （3）如图3，在（1）的条件下，O表示原点，动点P、T分别从C、O两点同时出发向左运动，同时动点R从点A出发向右运动，点P、T、R的速度分别为5个单位长度/秒、1个单位长度/秒、2个单位长度/秒，在运动过程中，如果点M为线段PT的中点，点N为线段OR的中点．请问PT-MN的值是否会发生变化？若不变，请求出相应的数值；若变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．下表是二次函数y=ax2+bx+c（ a≠0）图象上部分点的横坐标（x）和纵坐标（y）．
    x…-101234 5…
    y…830-10 m8…
    （1）观察表格，直接写出m=3；
    （2）其中A（x1，y1）、B（x2，y2）在函数的图象上，且-1＜x1＜0，2＜x2＜3，则y1＞y2（用“＞”或“＜”填空）；
    （3）求这个二次函数的表达式．

    查看答案和解析>>

    同步练习册答案