


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
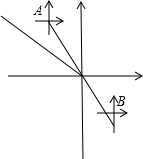 如图,学校操场的草地边有A、B两棵大树,小明把一颗珠子藏在草丛中,然后告诉王刚说:“站在藏珠子的地方可看见大树A在北偏西40°方向上,可看见大树B在南偏东60°方向上”,请同学们想一想:王刚能找到珠子吗?为什么?
如图,学校操场的草地边有A、B两棵大树,小明把一颗珠子藏在草丛中,然后告诉王刚说:“站在藏珠子的地方可看见大树A在北偏西40°方向上,可看见大树B在南偏东60°方向上”,请同学们想一想:王刚能找到珠子吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com