
【题目】△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α(0°<α≤90°),点F,G,P分别是DE,BC,CD的中点,连接PF,PG.
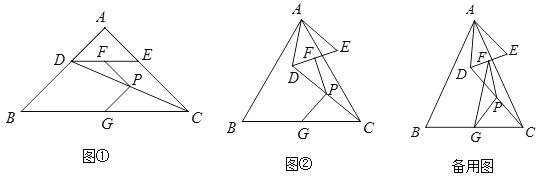
(1)如图①,α=90°,点D在AB上,则∠FPG= °;
(2)如图②,α=60°,点D不在AB上,判断∠FPG的度数,并证明你的结论;
(3)连接FG,若AB=5,AD=2,固定△ABC,将△ADE绕点A旋转,当PF的长最大时,FG的长为 (用含α的式子表示).
【答案】(1)90°;(2)120°,证明见解析;(3)![]() .
.
【解析】
(1)由AB=AC、AD=AE,得BD=CE,再根据G、P、F分别是BC、CD、DE的中点,可得出PG∥BD,PF∥CE.则∠GPF=180°﹣∠α=90°;
(2)连接BD,连接CE,由已知可证明△ABD≌△ACE,则∠ABD=∠ACE.因为G、P、F分别是BC、CD、DE的中点,则PG∥BD,PF∥CE.进而得出∠GPF=180°﹣∠α=120°;
(3)当D在BA的延长线上时,CE=BD最长,此时BD=AB+AD=5+2=7,再由三角形中位线定理即可算出PG=3.5,在Rt△GPH中,由三角函数的定义即可求出GH,进一步求出FG.
解:(1)∵AB=AC、AD=AE,∴BD=CE,
∵G、P、F分别是BC、CD、DE的中点,
∴PG∥BD,PF∥CE.∴∠ADC=∠DPG,∠DPF=∠ACD,
∠GPF=∠DPF+∠DPG=∠ADC+∠ACD=180°﹣∠BAC=180°﹣∠α=90°,
即∠GPF=90°;
故答案为:90;
(2)∠FPG=120°;
理由:连接BD,连接CE.
∵∠BAC=∠DAE,∴∠BAD=∠CAE,
在△ABD和△ACE中,
∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,
∵G、P、F分别是BC、CD、DE的中点,
∴PG∥BD,PF∥CE.∴∠PGC=∠CBD,
∠DPF=∠DCE=∠DCA+∠ACE=∠DCA+∠ABD,
∠DPG=∠PGC+∠BCD=∠CBD+∠BCD,
∠GPF=∠DPF+∠DPG=∠DCA+∠ABD+∠CBD+∠BCD=180°﹣∠BAC=180°﹣∠α=120°,即∠GPF==120°;
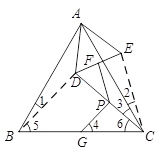
(3)连结BD,CE,过P作PH⊥FG于H,
由(2)可知,△ABD≌△ACE,∴BD=CE,且PG=PF=![]() BD,当D在BA的延长线上时,CE最长,即BD最长,此时BD=AB+AD=5+2=7,
BD,当D在BA的延长线上时,CE最长,即BD最长,此时BD=AB+AD=5+2=7,
∴PG=3.5,∵PF=PG,PH⊥FG,
∴∠GPH=![]() ∠FPG=
∠FPG=![]() (180°﹣∠α)=90°﹣
(180°﹣∠α)=90°﹣![]() α,FG=2HG,
α,FG=2HG,
∴FG=2HG=2PGsin∠GPH=2×3.5×![]() =
=![]() .
.
故答案为:![]() .
.



科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.
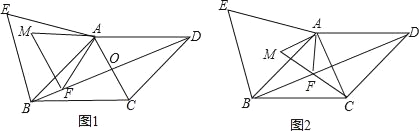
(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC=![]() AM;
AM;
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在笔山银子岩坡顶![]() 处的同一水平面上有一座移动信号发射塔
处的同一水平面上有一座移动信号发射塔![]() ,
,
笔山职中数学兴趣小组的同学在斜坡底![]() 处测得该塔的塔顶
处测得该塔的塔顶![]() 的仰角为
的仰角为![]() ,然后他们沿着坡度为
,然后他们沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该塔的塔顶
处又测得该塔的塔顶![]() 的仰角为
的仰角为![]() .求:
.求:
![]() 坡顶
坡顶![]() 到地面
到地面![]() 的距离;
的距离;
![]() 移动信号发射塔
移动信号发射塔![]() 的高度(结果精确到
的高度(结果精确到![]() 米).
米).
(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+b过A(0,﹣3),B(5,2),直线l2:y=k2x+2.
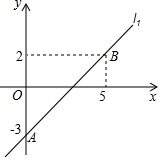
(1)求直线l1的表达式;
(2)当x≥4时,不等式k1x+b>k2x+2恒成立,请写出一个满足题意的k2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
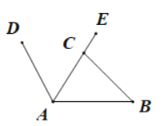
【题目】为倡导“绿色出行,低碳生活”的号召,今年春天,安庆市的街头出现了一道道绿色的风景线--“共享单车”. 图(1)所示的是一辆共享单车的实物图. 图(2)是这辆共享单车的部分几何示意图,其中车架档AC长为40cm,座杆CE的长为18cm. 点A、C、E在同一条直线上,且∠CAB=60°,∠ACB=75°
(1)求车座点E到车架档AB的距离;
(2)求车架档AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
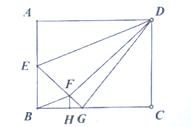
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,延长
,延长![]() 交
交![]() 于G,
于G,![]() ,垂足为H,连接
,垂足为H,连接![]() ,.以下结论:①
,.以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中正确的个数是()
;其中正确的个数是()
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
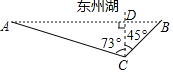
【题目】某市为了创建绿色生态城市,在城东建了“东州湖”景区,小明和小亮想测量“东州湖”东西两端A、B间的距离.于是,他们去了湖边,如图,在湖的南岸的水平地面上,选取了可直接到达点B的一点C,并测得BC=350米,点A位于点C的北偏西73°方向,点B位于点C的北偏东45°方向.请你根据以上提供的信息,计算“东州湖”东西两端之间AB的长.(结果精确到1米)(参考数据:sin73°≈0.9563,cos73≈0.2924,tan73°≈3.2709,![]() ≈1.414.)
≈1.414.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com