
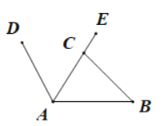
【题目】为倡导“绿色出行,低碳生活”的号召,今年春天,安庆市的街头出现了一道道绿色的风景线--“共享单车”. 图(1)所示的是一辆共享单车的实物图. 图(2)是这辆共享单车的部分几何示意图,其中车架档AC长为40cm,座杆CE的长为18cm. 点A、C、E在同一条直线上,且∠CAB=60°,∠ACB=75°
(1)求车座点E到车架档AB的距离;
(2)求车架档AB的长.

【答案】(1)车座点E到车架档AB的距离为![]() ;(2)车架档AB的长为
;(2)车架档AB的长为![]()
【解析】
(1)过E作EF⊥AB,垂足为F,运用EF=AE·sin∠CAB=58sin60°可得;
(2)过C作CG⊥AB,垂足为G,可得AG=AC·cos∠CAB=40cos60°,CG=AC·sin∠CAB=40sin60°,在Rt△BCG中,则BG=CG=![]() cm,故AB=AG+BG.
cm,故AB=AG+BG.
解(1)过E作EF⊥AB,垂足为F.
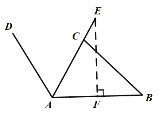
AE=AC+CE=58cm
在Rt△AEF中,∠CAB=60°,AE=58cm,
∴EF=AE·sin∠CAB=58sin60°=![]() cm.
cm.
答:车座点E到车架档AB的距离为![]()
(2)过C作CG⊥AB,垂足为G,
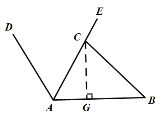
在Rt△ACG中,∠CAB=60°,AC=40cm,
则∠ACG=30°,∠BCG=∠ACB-∠ACG=45°
AG=AC·cos∠CAB=40cos60°=20cm
CG=AC·sin∠CAB=40sin60°=![]() cm
cm
在Rt△BCG中,∠BCG=45°,CG=![]() cm
cm
则BG=CG=![]() cm
cm
∴AB=AG+BG=(![]() )cm
)cm
答:车架档AB的长为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的一个交点为点
轴的一个交点为点![]() ,与
,与![]() 轴的交点为点
轴的交点为点![]() ,抛物线的对称轴
,抛物线的对称轴![]() 与
与![]() 轴交于点
轴交于点![]() ,与线段
,与线段![]() 交于点
交于点![]() ,点
,点![]() 是对称轴
是对称轴![]() 上一动点.
上一动点.

(1)点![]() 的坐标是________,点
的坐标是________,点![]() 的坐标是________;
的坐标是________;
(2)是否存在点![]() ,使得
,使得![]() 和
和![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
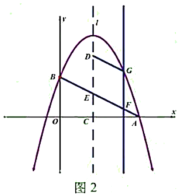
(3)如图2,抛物线的对称轴![]() 向右平移与线段
向右平移与线段![]() 交于点
交于点![]() ,与抛物线交于点
,与抛物线交于点![]() ,当四边形
,当四边形![]() 是平行四边形且周长最大时,求出点
是平行四边形且周长最大时,求出点![]() 的横坐标.
的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α(0°<α≤90°),点F,G,P分别是DE,BC,CD的中点,连接PF,PG.
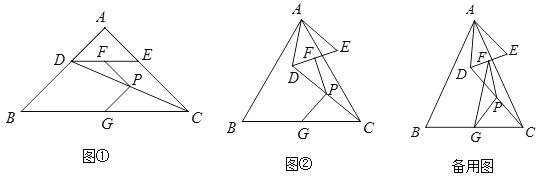
(1)如图①,α=90°,点D在AB上,则∠FPG= °;
(2)如图②,α=60°,点D不在AB上,判断∠FPG的度数,并证明你的结论;
(3)连接FG,若AB=5,AD=2,固定△ABC,将△ADE绕点A旋转,当PF的长最大时,FG的长为 (用含α的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是( ).

A. 甲的数学成绩高于班级平均分,且成绩比较稳定
B. 乙的数学成绩在班级平均分附近波动,且比丙好
C. 丙的数学成绩低于班级平均分,但成绩逐次提高
D. 就甲、乙、丙三个人而言,乙的数学成绩最不稳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
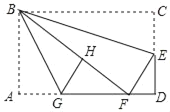
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处,点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②S△ABG=![]() S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正确的是_____.(把所有正确结论的序号都选上)
S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正确的是_____.(把所有正确结论的序号都选上)
查看答案和解析>>
科目:初中数学 来源: 题型:
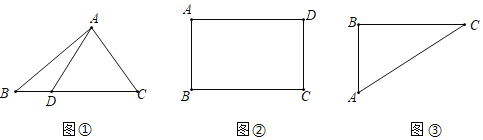
【题目】问题提出(1)如图①,在△ABC中,BC=6,D为BC上一点,AD=4,则△ABC面积的最大值是 .
问题探究(2)如图②,已知矩形ABCD的周长为12,求矩形ABCD面积的最大值.
问题解决(3)如图③,△ABC是葛叔叔家的菜地示意图,其中AB=30米,BC=40米,AC=50米,现在他想利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.已知葛叔叔欲建的鱼塘是四边形ABCD,且满足∠ADC=60°.你认为葛叔叔的想法能否实现?若能,求出这个四边形鱼塘周长的最大值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com