
【题目】如图,在△ABC中,∠A=∠B=30°,过点C作CD⊥AC,交AB于点D.
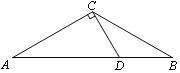
(1)作⊙O,使⊙O经过A、C、D三点(尺规作图,保留作图痕迹,不写作法);
(2)判断直线 BC与⊙O的位置关系,并说明理由.
科目:初中数学 来源: 题型:
【题目】学校准备为“中国古诗词”朗诵比赛购买奖品.已知在中央商场购买3个甲种奖品和2个乙种奖品共需120元;购买5个甲种奖品和4个乙种奖品共需210元.
(1)求甲、乙两种奖品的单价;
(2)学校计划购买甲、乙两种奖品共80个,且此次购买奖品的费用不超过1500元.正逢中央商场促销,所有商品一律八折销售,求学校在中央商场最多能购买多少个甲种奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为报答当年5.12汶川地震各地的驰援深情,四川某农产品公司决定将本公司农业基地生产的蔬菜水果全部运到湖北武汉,支援武汉人民抗击新冠疫情.为了运输的方便,将蔬菜和水果分别打包成件,蔬菜和水果共260件,蔬菜比水果多40件.
(1)求打包成件的蔬菜和水果各多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批物资全部运往武汉.已知甲种货车最多可装蔬菜30件和水果13件,乙种货车最多可装蔬菜和水果各15件.如果甲种货车每辆需付运输费3000元,乙种货车每辆需付运输费2400元.则公司安排甲、乙两种货车时有几种方案?并说明公司选择哪种方案可使运输费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在扇形![]() 中,
中,![]() ,半径
,半径![]() ,点P为
,点P为![]() 上任一点(不与A、O重合).
上任一点(不与A、O重合).
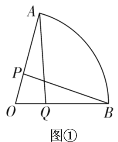
(1)如图①,Q是![]() 上一点,若
上一点,若![]() ,求证:
,求证:![]() .
.
(2)如图②,将扇形沿![]() 折叠,得到O的对称点
折叠,得到O的对称点![]() .
.
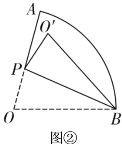
①若点![]() 落在
落在![]() 上,求
上,求![]() 的长;
的长;
②当![]() 与扇形
与扇形![]() 所在的圆相切时,求折痕的长.(注:本题结果不取近似值)
所在的圆相切时,求折痕的长.(注:本题结果不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
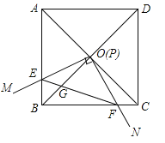
【题目】已知:如图,四边形ABCD是边长为1的正方形,对角线AC、BD相交于点O.过点O作一直角∠MON,直角边OM、ON分别与OA、OB重合,然后逆时针旋转∠MON,旋转角为θ(0°<θ<90°),OM、ON分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是________(填序号).
①![]() ;②S四边形OEBF:S正方形ABCD=1:2;③
;②S四边形OEBF:S正方形ABCD=1:2;③![]() ;④OGBD=AE2+CF2;⑤在旋转过程中,当△BEF与△COF的面积之和最大时,
;④OGBD=AE2+CF2;⑤在旋转过程中,当△BEF与△COF的面积之和最大时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王芳同学到文具店购买中性笔和笔记本,中性笔每支1元,笔记本每本3元,王芳同学现有10元钱,则可供她选择的购买方案的个数为(两样都买,余下的钱少于1元)( )
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把分子为1的分数叫做单位分数,如:![]() ,
,![]() ,
,![]() ,任何一个单位分数都可以拆分成两个不同的单位分数的和,如“
,任何一个单位分数都可以拆分成两个不同的单位分数的和,如“![]() =
=![]() +
+![]() ”,“
”,“![]() =
=![]() +
+![]() ”……
”……
(1)根据对上述式子的观察,你会发现.![]() =
=![]() ·请将问题中的空格补充完整.
·请将问题中的空格补充完整.
(2)进一步思考,单位分数![]() (n是不小于2的正整数),请写出■和●所表示的代数式,并对你的结论进行验证.
(n是不小于2的正整数),请写出■和●所表示的代数式,并对你的结论进行验证.
(3)请用(2)中你找出的规律解方程![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
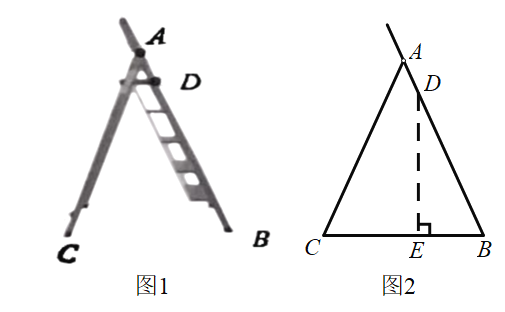
【题目】人字折叠梯完全打开后如图1所示,B,C是折叠梯的两个着地点,D是折叠梯最高级踏板的固定点.图2是它的示意图,AB=AC,BD=140cm,∠BAC=40°,求点D离地面的高度DE.(结果精确到0.1cm;参考数据sin70°≈0. 94,cos70°≈0.34,sin20°≈0.34,cos20°≈0.94)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com