
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
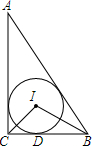 如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I与BC相切于点D,∠BIC=105°,AB=8cm,求:
如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I与BC相切于点D,∠BIC=105°,AB=8cm,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 美国圣路易斯市有一座巨大的拱门,这座拱高和底宽都是192m的不锈钢拱门是美国开发西部的标志性建筑.如果把拱门看作一条抛物线,试建立恰当的平面直角坐标系,并写出与该抛物线相应的函数表达式.
美国圣路易斯市有一座巨大的拱门,这座拱高和底宽都是192m的不锈钢拱门是美国开发西部的标志性建筑.如果把拱门看作一条抛物线,试建立恰当的平面直角坐标系,并写出与该抛物线相应的函数表达式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com