
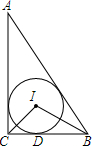
 如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I与BC相切于点D,∠BIC=105°,AB=8cm,求:
如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I与BC相切于点D,∠BIC=105°,AB=8cm,求:分析 (1)连接AI.三角形的内心即三条角平分线的交点,故此∠ICB=45°,由∠CIB=105°可知∠CBI=30°,于是得到∠CBA=60°,∠CAB=30°,∠AIB=135°;
(2)由题意可知AB=8,∠CAB=30°,依据特殊锐角三角函数值可求得BC=4,AC=4$\sqrt{3}$;
(3)根据三角形的面积=$\frac{1}{2}×$三角形的周长×内切圆的半径可求得r的值,连接ID,由∠IBD=30°可知:IB=2r.
解答 解:(1)连接AI.
∵∠ACB=90°,I是△ABC的内心,
∴∠ICB=45°.
又∵∠CIB=105°,
∴∠CBI=30°.
∴∠CBA=60°.
∴∠CAB=30°.
∴∠AIB=180°-$\frac{1}{2}×30°-\frac{1}{2}×60°$=135°.
(2)∵AB=8,∠CAB=30°,
∴BC=$\frac{1}{2}AB$=4,AC=AB×$\frac{\sqrt{3}}{2}$=4$\sqrt{3}$.
(3)设圆I的半径为r.根据题意得:$\frac{1}{2}×(4+8+4\sqrt{3})r$=$\frac{1}{2}×4×4\sqrt{3}$.
解得:r=2$\sqrt{3}$-2.
连接ID.
∵BC是圆I的切线,
∴ID⊥BC.
又∵∠IBD=30°.
∴IB=2ID=4$\sqrt{3}$-4.
点评 本题主要考查的是三角形的内心、特殊锐角三角函数,三角形的内角和定理,明确三角形的面积=$\frac{1}{2}×$三角形的周长×内切圆的半径是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
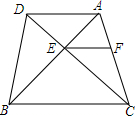 如图,在四边形ABCD中,CD交AB于点E,且AE:EB=1:2,EF∥BC∥AD,EF交AC于点F,S△ADE=1,求S△AEF和S△BCE.
如图,在四边形ABCD中,CD交AB于点E,且AE:EB=1:2,EF∥BC∥AD,EF交AC于点F,S△ADE=1,求S△AEF和S△BCE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
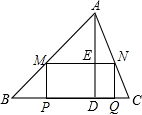 在锐角△ABC中,BC=6,S△ABC=12,矩形MPQN的两个顶点M,N分别在AB,AC上,另两个顶点P,Q均在BC上,高AD交MN于点E,设MN的长为x,矩形MPQN的面积为y.
在锐角△ABC中,BC=6,S△ABC=12,矩形MPQN的两个顶点M,N分别在AB,AC上,另两个顶点P,Q均在BC上,高AD交MN于点E,设MN的长为x,矩形MPQN的面积为y.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com