
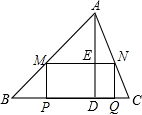
 在锐角△ABC中,BC=6,S△ABC=12,矩形MPQN的两个顶点M,N分别在AB,AC上,另两个顶点P,Q均在BC上,高AD交MN于点E,设MN的长为x,矩形MPQN的面积为y.
在锐角△ABC中,BC=6,S△ABC=12,矩形MPQN的两个顶点M,N分别在AB,AC上,另两个顶点P,Q均在BC上,高AD交MN于点E,设MN的长为x,矩形MPQN的面积为y.分析 (1)利用三角形的面积计算公式求得高AD即可;证得△AMN∽△ABC,得出$\frac{AE}{AD}$=$\frac{MN}{BC}$,进一步字母与数值得出答案即可;
(2)利用矩形的面积计算方法求得y关于x的函数解析式;
(3)利用二次函数的性质和配方法求得最大值即可.
解答 解:(1)∵S△ABC=12,
∴$\frac{1}{2}$BC•AD=12,又BC=6,
∴AD=4;
∵MN∥BC,
∴△AMN∽△ABC,
∴$\frac{AE}{AD}$=$\frac{MN}{BC}$,
即$\frac{AE}{4}$=$\frac{x}{6}$,
∴AE=$\frac{2}{3}$x;
(2)∵AE=$\frac{2}{3}$x,
∴MP=AD-AE=4-$\frac{2}{3}$x,
∴矩形MPQN的面积为y=x(4-$\frac{2}{3}$x)=-$\frac{2}{3}$x2+4x;
(3)∵y=-$\frac{2}{3}$x2+4x=-$\frac{2}{3}$(x-3)2+6,
∴当x=3时,y的最大值是6.
点评 本题主要考查了相似三角形的判定与性质,二次函数的性质,掌握对应高的比等于对应边的比的性质是正确列出比例式解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
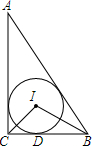 如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I与BC相切于点D,∠BIC=105°,AB=8cm,求:
如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I与BC相切于点D,∠BIC=105°,AB=8cm,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
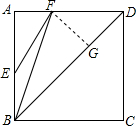 已知:如图,E、F分别是正方形ABCD的边AB和AD上的点,且$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$.求证:∠AEF=∠FBD.
已知:如图,E、F分别是正方形ABCD的边AB和AD上的点,且$\frac{EB}{AB}$=$\frac{AF}{AD}$=$\frac{1}{3}$.求证:∠AEF=∠FBD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 美国圣路易斯市有一座巨大的拱门,这座拱高和底宽都是192m的不锈钢拱门是美国开发西部的标志性建筑.如果把拱门看作一条抛物线,试建立恰当的平面直角坐标系,并写出与该抛物线相应的函数表达式.
美国圣路易斯市有一座巨大的拱门,这座拱高和底宽都是192m的不锈钢拱门是美国开发西部的标志性建筑.如果把拱门看作一条抛物线,试建立恰当的平面直角坐标系,并写出与该抛物线相应的函数表达式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x2+1)(x-1) | B. | (x-1)2 | C. | (x-1)2(x2+1) | D. | (x2-1)(x2+1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数的解析式是y=x2-2x-3.
已知二次函数的解析式是y=x2-2x-3.| x | … | … | |||||
| y | … | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com