
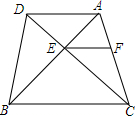
 如图,在四边形ABCD中,CD交AB于点E,且AE:EB=1:2,EF∥BC∥AD,EF交AC于点F,S△ADE=1,求S△AEF和S△BCE.
如图,在四边形ABCD中,CD交AB于点E,且AE:EB=1:2,EF∥BC∥AD,EF交AC于点F,S△ADE=1,求S△AEF和S△BCE. 分析 已知AD∥EF∥BC,根据平行线分线段成比例定理,可得出AE:EB=AF:FC,也就求出EF与AD的比例关系;由于△ADE和△AEF等高,因此它们的面积比等于底边比,已知了EF、AD的比例关系,根据△ADE的面积即可求出△AEF、△BCE的面积.
解答 解:∵DA∥BC,
∴△ADE∽△BCE.
∴S△ADE:S△BCE=AE2:BE2.
∵AE:BE=1:2,
∴S△ADE:S△BCE=1:4.
∵S△ADE=1,
∴S△BCE=4.
∵S△ABC:S△BCE=AB:BE=3:2,
∴S△ABC=6.
∵EF∥BC,
∴△AEF∽△ABC.
∵AE:AB=1:3,
∴S△AEF:S△ABC=AE2:AB2=1:9.
∴S△AEF=$\frac{2}{3}$.
点评 本题主要考查了平行线分线段成比例定理以及三角形的面积的计算公式.注意,同底(或等底)三角形的面积比等于该底上的高的比;同高(或等高)三角形的面积比等于对应底边的比.当两个三角形相似时,它们的面积比等于对应线段比的平方,即相似比的平方.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
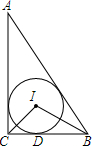 如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I与BC相切于点D,∠BIC=105°,AB=8cm,求:
如图,在Rt△ABC中,∠ACB=90°,内切圆⊙I与BC相切于点D,∠BIC=105°,AB=8cm,求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知E、F分别是正方形ABCD的边BC、DC上的点,且∠EAF=45°,自E、F分别作AC的垂线,垂足为P、Q,求证:AB2=AP•AQ.
已知E、F分别是正方形ABCD的边BC、DC上的点,且∠EAF=45°,自E、F分别作AC的垂线,垂足为P、Q,求证:AB2=AP•AQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 美国圣路易斯市有一座巨大的拱门,这座拱高和底宽都是192m的不锈钢拱门是美国开发西部的标志性建筑.如果把拱门看作一条抛物线,试建立恰当的平面直角坐标系,并写出与该抛物线相应的函数表达式.
美国圣路易斯市有一座巨大的拱门,这座拱高和底宽都是192m的不锈钢拱门是美国开发西部的标志性建筑.如果把拱门看作一条抛物线,试建立恰当的平面直角坐标系,并写出与该抛物线相应的函数表达式.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
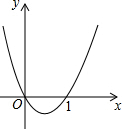 如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②a<0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②a<0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )| A. | ①④ | B. | ②③④ | C. | ③④⑤ | D. | ①③⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com