
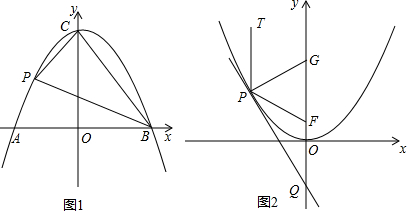
·ÖÎö £¨1£©ÏÈÀûÓĂ¡ÏABCµÄƠưÇĐÖµÇó³öOCµÄ³¤£¬µĂµ½µăCµÄ×ø±ê£¬È»ºóÀûÓĂ´ư¶¨ÏµÊư·¨Çó½â¼´¿É£»
£¨2£©·ÖÁ½ÖÖÇé¿ö£º¢ÙµăPÔÚyÖáµÄ×ó²à£¬¢ÚµăPÔÚyÖáµÄÓ̉²à£¬·Ö±đÇó³öSµÄÈ¡Öµ·¶Î§£¬È»ºó½áºÏSΪƠûÊư£¬Ở³öµăPµÄ¸öÊư£¬¼´¿ÉµĂ³ö´đ°¸£»
£¨3£©ÏÈÀûÓö₫´Îº¯ÊưµÄͼÏóÓ뼸ºÎ±ä»»µĂ³öÅ×ÎïÏßC2µÄ½âÎöʽ£¬²¢ÉèP£¨m£¬$\frac{1}{4}$m2£©£¬Ö±ÏßPQµÄ½âÎöʽΪy=kx+n£¨k¡Ù0£©£¬¸ù¾ƯÖ±ÏßPQÓëÅ×ÎïÏßÓĐ̉»¸ö½»µăÇóµĂn=-k2£¬È»ºóÓĂk±íʾµăP¡¢Q¡¢GµÄ×ø±ê£¬µĂµ½GF=FQ£¬ÔÙÀûÓĂÖ±½ÇÈư½ÇĐÎб±ßÉϵÄÖĐÏßµÄĐÔÖÊ£¬µÈÑüÈư½ÇĐεÄĐÔÖʺÍƽĐĐÏßµÄĐÔÖʽøĐĐÍÆÀí¼´¿É£®
½â´đ ½â£º£¨1£©ÓÉB£¨6£¬0£©¿ÉµĂOB=6£¬
¡ßtan¡ÏABC=$\frac{OC}{OB}$=$\frac{OC}{6}$=$\frac{4}{3}$£¬
¡àOC=8£¬µăCµÄ×ø±êΪ£¨0£¬8£©£¬
¡ßµăA¡¢B¡¢CÈưµăÔÚÅ×ÎïÏßC1ÉÏ£¬
¡à$\left\{\begin{array}{l}{\frac{256}{9}a-\frac{16}{3}b+c=0}\\{36a+6b+c=0}\\{c=8}\end{array}\right.$£¬½âµĂ$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{1}{6}}\\{c=8}\end{array}\right.$£¬
¡àÅ×ÎïÏßC1µÄ½âÎöʽΪy=-$\frac{1}{4}$x2+$\frac{1}{6}$x+8£»
£¨2£©¢Ùµ±µăPÔÚyÖáµÄ×ó²àʱ£¬´ËʱµăPµÄºá×ø±êxÂú×ă-$\frac{16}{3}$£¼x£¼0£¬
ÈôPÓëµăAÖغϣ¬Ộ¡÷PBCµÄĂæ»ưΪS=$\frac{1}{2}$¡Á£¨$\frac{16}{3}$+6£©¡Á8=45$\frac{1}{3}$£¬
¡àSµÄÈ¡Öµ·¶Î§ÊÇ0£¼S£¼45$\frac{1}{3}$£¬
¡ßSΪƠûÊư£¬
¡àS¿ÉÈ¡µÄֵΪ1£¬2£¬¡45£¬¹²45¸ö£¬
ÓÖ¡ßµăPµÄºá×ø±êxÂú×ă-$\frac{16}{3}$£¼x£¼0£¬
¡àµăPÓĐ45¸öλÖĂ£¬
¡àµăPÔÚyÖáµÄ×ó²àÇ̉¡÷PBCµÄĂæ»ưSΪƠûÊưʱ£¬¡÷PBCÓĐ45¸ö£»
¢Úµ±µăPÔÚyÖáµÄÓ̉²àʱ£¬´ËʱµăPµÄºá×ø±êxÂú×ă0£¼x£¼6£¬
Èçͼ£¬Á¬½ÓOP£¬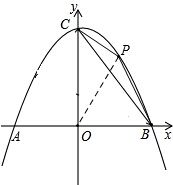
ÉèµăPµÄ×ø±êΪ£¨x£¬-$\frac{1}{4}$x2+x+8£©£¬
¡àS=S¡÷PCO+S¡÷POB-S¡÷OBC
=$\frac{1}{2}$¡Á8•x+$\frac{1}{2}$¡Á6£¨-$\frac{1}{4}$x2+x+8£©-$\frac{1}{2}$¡Á6¡Á8
=-$\frac{3}{4}$£¨x-3£©2+6$\frac{3}{4}$£¬
¡àSµÄÈ¡Öµ·¶Î§ÊÇ0£¼S£¼6$\frac{3}{4}$£¬
¡ßSΪƠûÊư£¬
¡àS¿ÉÈ¡µÄֵΪ1£¬2£¬¡6£¬¹²6¸ö£¬
ÓÖ¡ßµăPµÄºá×ø±êxÂú×ă0£¼x£¼6£¬
¡àµăPÓĐ12¸öλÖĂ£¬
¡àµăPÔÚyÖáµÄÓ̉²àÇ̉¡÷PBCµÄĂæ»ưSΪƠûÊưʱ£¬¡÷PBCÓĐ12¸ö£»
×ۺϢ١¢¢Ú¿ÉÖª£¬ƠâÑùµÄ¡÷PBC¹²ÓĐ45+12=57¸ö£»
£¨3£©¡ßÅ×ÎïÏßC1ÈÆ×ÅijµăĐưת180¡ă£¬µĂµ½µÄĐÂÅ×ÎïÏßC2µÄ¶¥µăΪ×ø±êÔµă£¬
¡àĐÂÅ×ÎïÏßC2µÄ½âÎöʽΪy=$\frac{1}{4}$x2£¬
ÉèP£¨m£¬$\frac{1}{4}$m2£©£¬Ö±ÏßPQµÄ½âÎöʽΪy=kx+n£¨k¡Ù0£©£¬
ÓɵăQÊÇyÖḺ°ëÖáÉÏ̉»µă£¬¹ưQµăµÄÖ±ÏßPQÓëÅ×ÎïÏßC2ÔÚµÚ¶₫ÏóÏ̃ÓĐΨ̉»¹«¹²µăP£¬µĂ$\left\{\begin{array}{l}{y=\frac{1}{4}{x}^{2}}\\{y=kx+n}\end{array}\right.$£¬
¡à$\frac{1}{4}$x2-kx+n=0£¬
¡à¡÷=£¨-k£©2-4¡Á$\frac{1}{4}$¡Á£¨-n£©=0£¬¡àn=-k2£¬
¡àÖ±ÏßPQµÄ½âÎöʽΪy=kx-k2£¬P£¨2k£¬k2£©£¬Q£¨0£¬-k2£©£¬
ÉèÖ±ÏßPGµÄ½âÎöʽΪy=-$\frac{1}{k}$x+p£¬½«PµÄ×ø±ê´úÈë¿ÉµĂp=k2+2£¬ỘG£¨0£¬k2+2£©£¬
¡àGF=k2+1£¬FQ=k2+1£¬
¡àGF=FQ£¬¼´µăFÊÇRt¡÷GPQб±ßÉϵÄÖĐµă£¬
¡àFP=FG£¬
¡à¡ÏFPG=¡ÏFGP£¬
ÓÖ¡ßPT¡ÎyÖᣬ
¡à¡ÏTPG=¡ÏFGP£¬
¡à¡ÏTPG=¡ÏFPG£®
µăÆÀ ±¾̀⿼²éÁ˶₫´Îº¯ÊưµÄ×ÛºÏÓ¦ÓĂ£¬Éæ¼°ÁË´ư¶¨ÏµÊư·¨Çó̉»´Îº¯Êư¡¢¶₫´Îº¯ÊưµÄ½âÎöʽ£¬Èư½ÇĐεÄĂæ»ư£¬Ö±½ÇÈư½ÇĐεÄĐÔÖʵÈ֪ʶ£¬×ÛºÏĐÔ½ÏÇ¿£¬ÓĐ̉»¶¨µÄÄѶȣ¬½ầâʱ̉ª×¢̉âÊưĐνáºÏ˼Ï룬·½³̀˼Ï룬·ÖÀà̀ÖÂÛ˼ÏëµÄÓ¦ÓĂ£®



| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
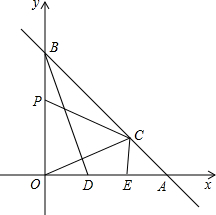 Èçͼ£¬Ö±ÏßL½»xÖá¡¢yÖá·Ö±đÓÚA¡¢BÁ½µă£¬A£¨a£¬0£©B£¨0£¬b£©£¬Ç̉£¨a-b£©2+|b-4|=0
Èçͼ£¬Ö±ÏßL½»xÖá¡¢yÖá·Ö±đÓÚA¡¢BÁ½µă£¬A£¨a£¬0£©B£¨0£¬b£©£¬Ç̉£¨a-b£©2+|b-4|=0²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
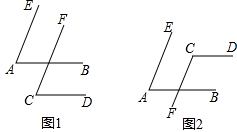
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
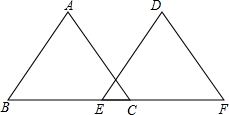 Èçͼ£ºB¡¢E¡¢C¡¢FËĵăÔÚͬ̉»Ö±ÏßÉÏ£¬Ç̉¡ÏACB=¡ÏF£¬¡ÏB=¡ÏDEF£¬BE=CF£¬¡ÏA=50¡ă£¬Çó¡ÏDµÄ¶ÈÊư£¬²¢ËµĂ÷ÀíÓÉ£®
Èçͼ£ºB¡¢E¡¢C¡¢FËĵăÔÚͬ̉»Ö±ÏßÉÏ£¬Ç̉¡ÏACB=¡ÏF£¬¡ÏB=¡ÏDEF£¬BE=CF£¬¡ÏA=50¡ă£¬Çó¡ÏDµÄ¶ÈÊư£¬²¢ËµĂ÷ÀíÓÉ£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
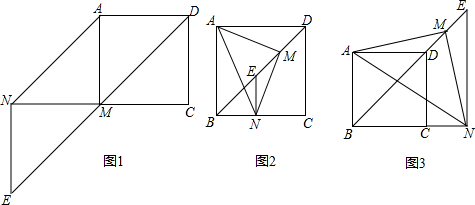
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
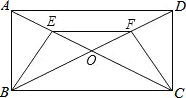 ¾ØĐÎABCDµÄ¶Ô½ÇÏßAC¡¢BDÏཻÓÚµăO£¬Ç̉AE=DF£®
¾ØĐÎABCDµÄ¶Ô½ÇÏßAC¡¢BDÏཻÓÚµăO£¬Ç̉AE=DF£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º̀î¿Ờâ
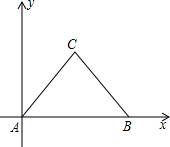 Èçͼ£¬µÈ±ß¡÷ABCÖĐ£¬µăAΪ×ø±êÔµă£¬µăBµÄ×ø±êΪ£¨6£¬0£©£¬ỘµăCµÄ×ø±êΪ£¨3£¬3$\sqrt{3}$£©»̣£¨3£¬-3$\sqrt{3}$£©£®
Èçͼ£¬µÈ±ß¡÷ABCÖĐ£¬µăAΪ×ø±êÔµă£¬µăBµÄ×ø±êΪ£¨6£¬0£©£¬ỘµăCµÄ×ø±êΪ£¨3£¬3$\sqrt{3}$£©»̣£¨3£¬-3$\sqrt{3}$£©£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º³ơÖĐÊưѧ À´Ô´£º ̀âĐÍ£º½â´đ̀â
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com