
【题目】下列叙述中:![]() 任意一个三角形的三条高至少有一条在此三角形内部;
任意一个三角形的三条高至少有一条在此三角形内部;![]() 以a,b,c为边
以a,b,c为边![]() b,c都大于0,且
b,c都大于0,且![]() 可以构成一个三角形;
可以构成一个三角形;![]() 一个三角形内角之比为3:2:1,此三角形为直角三角形;
一个三角形内角之比为3:2:1,此三角形为直角三角形;![]() 有两个角和一条边对应相等的两个三角形全等;正确的有
有两个角和一条边对应相等的两个三角形全等;正确的有![]()
![]() 个.
个.
A. 1B. 2C. 3D. 4
【答案】C
【解析】
锐角三角形的三条高都在三角形的内部,直角三角形有一条高在三角形的内部,两条在三角形的两边上,钝角三角形的一条高在三角形的内部,两条高在三角形的外部,根据以上内容即可判断①;举出反例a=2,b=c=1,满足a+b>c,但是边长为1、1、2不能组成三角形,即可判断②;设三角形的三角为3x°,2x°,x°,由三角形的内角和定理得:3x+2x+x=180,求出3x=90,得出三角形是直角三角形,即可判断③;根据有两个角和一条边对应相等的两个三角形全等即可判断④.
∵锐角三角形的三条高都在三角形的内部,直角三角形有一条高在三角形的内部,两条在三角形的两边上,钝角三角形的一条高在三角形的内部,两条高在三角形的外部,∴①正确;
∵当a=2,b=c=1时,满足a+b>c,但是边长为1、1、2不能组成三角形,∴②错误;
∵设三角形的三角为3x°,2x°,x°,∴由三角形的内角和定理得:3x+2x+x=180,∴x=30,3x=90,即三角形是直角三角形,∴③正确;
∵有两个角和一条边对应相等的两个三角形全等,∴④正确.
故选C.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】阅读:
我们知道,![]() 于是要解不等式
于是要解不等式![]() ,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:
,我们可以分两种情况去掉绝对值符号,转化为我们熟悉的不等式,按上述思路,我们有以下解法:
解:(1)当![]() ,即
,即![]() 时:
时:![]()
解这个不等式,得:![]()
由条件![]() ,有:
,有:![]()
(2)当![]() ,即
,即![]() 时,
时,![]()
解这个不等式,得:![]()
由条件![]() ,有:
,有:![]()
∴ 如图,![]()
综合(1)、(2)原不等式的解为:![]()
根据以上思想,请探究完成下列![]() 个小题:
个小题:
![]() ;
;
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中, ![]() 三个顶点坐标分别为
三个顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)请画出![]() 关于
关于![]() 轴对称的图形
轴对称的图形![]() ;
;
(2)将![]() 的三个顶点的横坐标与纵坐标同时乘
的三个顶点的横坐标与纵坐标同时乘![]() ,得到对应的点
,得到对应的点![]() 、
、![]() 、
、![]() ,请画出
,请画出![]()
![]() ;
;
(3)求![]() 与
与![]() 的面积比,即
的面积比,即![]() :
:![]() =________(不写解答过程,直接写出结果).
=________(不写解答过程,直接写出结果).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a是一个长为![]() 、宽为
、宽为![]() 的长方形(其中
的长方形(其中![]() >
>![]() ), 沿图中虚线用剪刀均分成四块小长方形, 然后按图
), 沿图中虚线用剪刀均分成四块小长方形, 然后按图![]() 的形状拼成一个正方形,
的形状拼成一个正方形,
(1)①请你用两种不同的方法表示图![]() 中的阴影部分的面积 ; ;
中的阴影部分的面积 ; ;
②请写出代数式:![]() ,
,![]() ,
,![]() 之间的关系: ;
之间的关系: ;
(2)若![]() ,求:
,求:![]() 的值;
的值;
(3)已知![]() ,求:
,求:![]() 的值.
的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60( ![]() +1)海里,在B处测得C在北偏东45°反向上,A处测得C在北偏西30°方向上,在海岸线AB上有一灯塔D,测得AD=100海里.
+1)海里,在B处测得C在北偏东45°反向上,A处测得C在北偏西30°方向上,在海岸线AB上有一灯塔D,测得AD=100海里.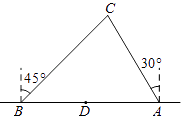
(1)分别求出AC,BC(结果保留根号).
(2)已知在灯塔D周围80海里范围内有暗礁群,在A处海监穿沿AC前往C处盘查,途中有无触礁的危险?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).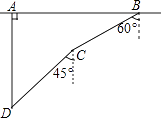
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com