Question

【题目】在ABCD中，E、F分别是AB、CD的中点，AF与DE相交于点G，CE与BF相交于点H．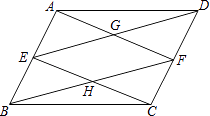

（1）求证：四边形EHFG是平行四边形；
（2）若四边形EHFG是矩形，则ABCD应满足什么条件？（不需要证明）

Answer 1

【答案】
（1）证明：∵四边形ABCD是平行四边形，

∴AE∥CF，AB=CD，

∵E是AB中点，F是CD中点，

∴AE=CF，

∴四边形AECF是平行四边形，

∴AF∥CE．

同理可得DE∥BF，

∴四边形FGEH是平行四边形

（2）解：当平行四边形ABCD是矩形，并且AB=2AD时，平行四边形EHFG是矩形．

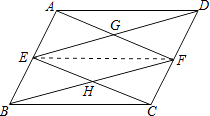
∵E，F分别为AB，CD的中点，且AB=CD，

∴AE=DF，且AE∥DF，

∴四边形AEFD为平行四边形，

∴AD=EF，

又∵AB=2AD，E为AB中点，则AB=2AE，

于是有AE=AD= AB，

这时，EF=AE=AD=DF= AB，∠EAD=∠FDA=90°，

∴四边形ADFE是正方形，

∴EG=FG= AF，AF⊥DE，∠EGF=90°，

∴此时，平行四边形EHFG是矩形．

【解析】（1）通过证明两组对边分别平行，可得四边形EHFG是平行四边形；
（2）当平行四边形ABCD是矩形，并且AB=2AD时，先证明四边形ADFE是正方形，得出有一个内角等于90°，从而证明菱形EHFG为一个矩形．

【考点精析】利用平行四边形的判定与性质和矩形的判定方法对题目进行判断即可得到答案，需要熟知若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积；有一个角是直角的平行四边形叫做矩形；有三个角是直角的四边形是矩形；两条对角线相等的平行四边形是矩形．