
����Ŀ����֪��������y��ax2��3��a��1��x+2a��6��a��0����
��1����֤����������x�����������㣮
��2������������x�����������ĺ�����ֱ�Ϊx1��x2������x1��x2������t�ǹ���a�ĺ�������t��ax2��x1������������ı���ʽ��
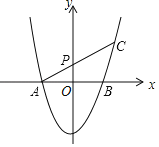
��3����a��1��������������ƽ��һ����λ����x�ύ�ڵ�A��B��ƽ�ƺ���ͼ��ʾ����A��ֱ��AC���ֱ�y���������ڵ�P���������ڵ�C����OP��1��M���߶�AC��һ���㣬��2MB+MC����Сֵ��
���𰸡���1�������������2��t��a��5����3��2MB+MC����СֵΪ![]() ��
��
��������
��1��Ҫ֤��������x�����������㣬�������Ӧ��һԪ���η��̵ĸ����б�ʽ��ֵ��������ȫƽ����ʽ�ķǸ���˵������0���ɣ�
��2����y��0�������a����������ĺ����꣬Ȼ���������ȷ��x2��x1���ٴ���t��ax2��x1���������ɣ�
��3�������ƽ�ƺ������ߵĽ���ʽ��A��B�������ֱ��AC�Ľ���ʽ��Ȼ������ֱ��AC�Ľ���ʽ�Ͷ��κ����Ľ���ʽ�ɵõ�C�����꣬��C��CN��y�ᣬ��M��MG��CN��G����C��CH��x����H���á�GCM��30������![]() ������2MB+MC��2��MB+GM������MB+GM����Сֵ��B��CN����С����CH�����⼴�ý����
������2MB+MC��2��MB+GM������MB+GM����Сֵ��B��CN����С����CH�����⼴�ý����
��1��֤��������b2��4ac��[��3��a��1��]2��4a��2a��6����a2+6a+9����a+3��2��
��a��0���ࣨa+3��2��0��
����������x�����������㣻
��2���⣺��y��0����ax2��3��a��1��x+2a��6��0��
��a��0����![]() ����x=2��
����x=2��![]() ��
��
��a��0����![]() ��
��
��x1��x2����x1��2��![]() ��
��
��![]() ��
��
��t��a��5��
��3���⣺��a��1ʱ��������Ϊy��x2��4������ƽ��һ����λ��y��x2��3��
��y��0����x2��3��0����ã�![]() ����A��
����A��![]() ��0����B��
��0����B��![]() ��0������AO��
��0������AO��![]() ��
��
��OP��1����P��0��1������ֱ��AC�Ľ���ʽΪ![]() ���ѵ�A��
���ѵ�A��![]() ��0�����룬�ã�
��0�����룬�ã�![]() ����ֱ��AC�Ľ���ʽΪ��
����ֱ��AC�Ľ���ʽΪ��![]() ��
��
������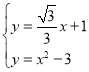 ����ã�
����ã�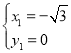 ��
�� �����C������
�����C������![]() ��
��![]() ����
����
��Rt��AOP�У����ݹ��ɶ������ã�AP��![]() ������OAP=30����
������OAP=30����
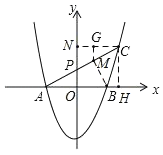
��C��CN��y�ᣬ��M��MG��CN��G����C��CH��x����H��
��CN��x�ᣬ���GCM����PAO=30������![]() ��
��
��![]() ��
��
��B��CN��С����ΪCH��
��MB+GM����СֵΪCH�ij���![]() ��
��
��2MB+MC����СֵΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ת����ת�̡�ÿ��ת�̱��ֳ���ͼ��ʾ�ļ������Ρ���Ϸ��ͬʱת������ת�̣����һ��ת��ת���˺�ɫ����һת��ת������ɫ����Ϸ�߾��������ɫ����˵����ȷ���ǣ�������
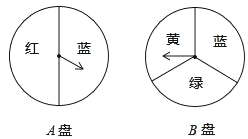
A. ����ת��ת����ɫ�ĸ���һ����
B. ���Aת��ת������ɫ����ôBת��ת����ɫ�Ŀ����Ա�С��
C. ��ת��A ת����ת��B ת�̺�ͬʱת������ת�̣���Ϸ�������ɫ�ĸ��ʲ�ͬ
D. ��Ϸ�������ɫ�ĸ���Ϊ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��![]() ����
����![]() ��
��![]() ���ϣ�����
���ϣ�����![]() ������
������![]() �ڹ�
�ڹ�![]() ����Ē������ϣ�
����Ē������ϣ�
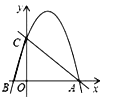
��1���������ߵĽ���ʽ��
��2������ֱ![]() ���ֱ�ߣ��ڵ�һ����ֱ��
���ֱ�ߣ��ڵ�һ����ֱ��![]() �ڵ�
�ڵ�![]() �����������ڵ�
�����������ڵ�![]() �����߶�
�����߶�![]() �ij������ֵʱ
�ij������ֵʱ![]() �����꣮�����
�����꣮�����![]() ���ֵ�Ƕ��٣�
���ֵ�Ƕ��٣�
��3����![]() �����Ƿ���ڵ�
�����Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() �ǵ���������?�����ڣ���ֱ��д����
�ǵ���������?�����ڣ���ֱ��д����![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
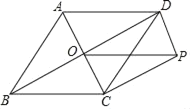
����Ŀ����ͼ��������ABCD�У�AC��BD���ڵ�O��BD��8��AC��4��DP��AC��CP��BD��
��1�����߶�OP�ij���
��2���������κθ����ߵ�����£�ֱ��д��ͼ�����е�ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�ƻ�����ѧ������Ȥ�����齨������ȤС�飬�������ȡ�˲���ͬѧ����Ȥ���ý��е��飬���ռ����������������Ƴ���������ͳ��ͼ�������ͼ�е���Ϣ������������⣺

![]() ѧУ��ε��鹲��ȡ�� ��ѧ����
ѧУ��ε��鹲��ȡ�� ��ѧ����
![]() ��
��![]() ��ֵ����ȫ����ͳ��ͼ��
��ֵ����ȫ����ͳ��ͼ��
![]() ������ͳ��ͼ�У���Χ�����������ε�Բ�ĽǶ���Ϊ ��
������ͳ��ͼ�У���Χ�����������ε�Բ�ĽǶ���Ϊ ��
![]() ���У����ѧ��
���У����ѧ��![]() ����������Ƹ�У�ж�����ѧ��ϲ������
����������Ƹ�У�ж�����ѧ��ϲ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ϣ�����ʦ�ó���4�ŷֱ���������1��2��3��4�Ŀ�Ƭ������������������ͬ������ͬѧ�������ȡ���ţ������������ſ�Ƭ�����ֵĺͣ�
��1�������б�����״ͼ�ķ����оٳ����еȿ��ܵĽ����
��2�������ſ�Ƭ�����ֵĺʹ���5�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10������Rt��ABC�У���BAC=![]() ,D��BC���е㣬E��AD���е�������A��AF��BC��BE���ӳ����ڵ�F��
,D��BC���е㣬E��AD���е�������A��AF��BC��BE���ӳ����ڵ�F��

��1����֤����AEF����DEB��
��2��֤���ı���ADCF�����Σ�
��3����AC=4��AB=5��������ADCFD �������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ���c��0����2a+b��0����a+b+c��0����b2��4ac��0��������ȷ���У� ��
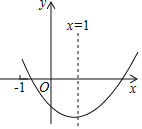
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ֱ��A��B����ͬʱ��������ͬһ����·�ϣ�������ʻ��������У�����������ʱֹͣ.�׳���ʻһ��ʱ������ͣ��0.5Сʱ�����Ͻ��������ԭ����B����ʻ������֮���·��y��ǧ�ף������������ʱ��x(Сʱ��֮��ĺ�����ϵ��ͼ��ʾ.

��1����ס���������ʻ���ٶ�V����V��.
��2����m��ֵ.
��3�����׳�û�й���ͣ�����������ǰ�ʱ����������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com