
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
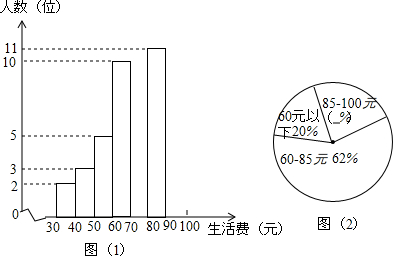
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
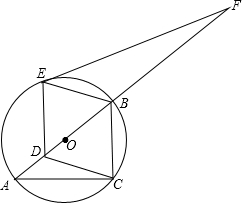 如图,点A,B,C在⊙O上,AB是⊙O的直径,AC=4,BC=3.
如图,点A,B,C在⊙O上,AB是⊙O的直径,AC=4,BC=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
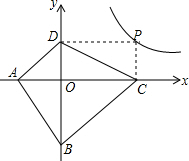 阅读理解:对于任意正实数a,b,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a=b时,a+b有最小值2$\sqrt{p}$.
阅读理解:对于任意正实数a,b,因为($\sqrt{a}$-$\sqrt{b}$)2≥0,∴a-2$\sqrt{ab}$+b≥0,∴a+b≥2$\sqrt{ab}$,当且仅当a=b时,等号成立.结论:在a+b≥2$\sqrt{ab}$(a,b均为正实数)中,若ab为定值p,则a+b≥2$\sqrt{p}$,当且仅当a=b时,a+b有最小值2$\sqrt{p}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
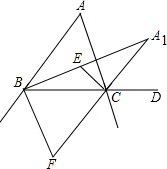 如图,在△ABC中,点E是∠ABC、∠ACB角平分线的交点,点F是∠ABC、∠ACB外角平分线的交点,点A1是内角∠ABC、外角∠ACD平分线的交点.
如图,在△ABC中,点E是∠ABC、∠ACB角平分线的交点,点F是∠ABC、∠ACB外角平分线的交点,点A1是内角∠ABC、外角∠ACD平分线的交点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com