
【题目】六一儿童节,小文到公园游玩.看到公园的一段人行弯道MN(不计宽度),如图,它与两面互相垂直的围墙OP、OQ之间有一块空地MPOQN(MP⊥OP,NQ⊥OQ),他发现弯道MN上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A、B、C是弯道MN上的三点,矩形ADOG、矩形BEOH、矩形CFOI的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S1、S2、S3 , 并测得S2=6(单位:平方米).OG=GH=HI. 
(1)求S1和S3的值;
(2)设T(x,y)是弯道MN上的任一点,写出y关于x的函数关系式;
(3)公园准备对区域MPOQN内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?
【答案】
(1)解:∵矩形ADOG、矩形BEOH、矩形CFOI的面积相等,
∴弯道为反比例函数图象的一部分,
设函数解析式为y= ![]() (k≠0),OG=GH=HI=a,
(k≠0),OG=GH=HI=a,
则AG= ![]() ,BH=
,BH= ![]() ,CI=
,CI= ![]() ,
,
所以,S2= ![]() a﹣
a﹣ ![]() a=6,
a=6,
解得k=36,
所以,S1= ![]() a﹣
a﹣ ![]() a=
a= ![]() k=
k= ![]() ×36=18,
×36=18,
S3= ![]() a=
a= ![]() k=
k= ![]() ×36=12;
×36=12;
(2)解:∵k=36,
∴弯道函数解析式为y= ![]() ,
,
∵T(x,y)是弯道MN上的任一点,
∴y= ![]() ;
;
(3)解:∵MP=2米,NQ=3米,
∴GM= ![]() =18,
=18, ![]() =3,
=3,
解得OQ=12,
∵在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),
∴x=2时,y=18,可以种8棵,
x=4时,y=9,可以种4棵,
x=6时,y=6,可以种2棵,
x=8时,y=4.5,可以种2棵,
x=10时,y=3.6,可以种1棵,
一共可以种:8+4+2+2+1=17棵.
答:一共能种植17棵花木.
【解析】(1)判断出弯道为反比例函数图象的一部分,设函数解析式为y= ![]() (k≠0),OG=GH=HI=a,然后表示出AG、BH、CI,再根据S2列出方程求出k,然后分别求解即可;(2)根据k值求解即可;(3)求出点Q的横坐标为12,再分别求出横坐标为偶数时的y值,然后计算种植的棵数即可.
(k≠0),OG=GH=HI=a,然后表示出AG、BH、CI,再根据S2列出方程求出k,然后分别求解即可;(2)根据k值求解即可;(3)求出点Q的横坐标为12,再分别求出横坐标为偶数时的y值,然后计算种植的棵数即可.


科目:初中数学 来源: 题型:
【题目】如图,BD为正方形ABCD的对角线,BE平分∠DBC,交DC与点E,将△BCE绕点C顺时针旋转90°得到△DCF,若CE=1cm,则BF=cm. 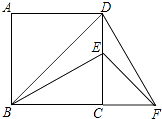
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】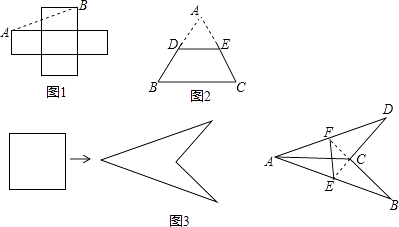
(1)阅读材料:
教材中的问题,如图1,把5个边长为1的小正方形组成的十字形纸板剪开,使剪成的若干块能够拼成一个大正方形,小明的思考:因为剪拼前后的图形面积相等,且5个小正方形的总面积为5,所以拼成的大正方形边长为 , 故沿虚线AB剪开可拼成大正方形的一边,请在图1中用虚线补全剪拼示意图 .
(2)类比解决:
如图2,已知边长为2的正三角形纸板ABC,沿中位线DE剪掉△ADE,请把纸板剩下的部分DBCE剪开,使剪成的若干块能够拼成一个新的正三角形.
拼成的正三角形边长为;
(3)在图2中用虚线画出一种剪拼示意图.
(4)灵活运用:
如图3,把一边长为60cm的正方形彩纸剪开,用剪成的若干块拼成一个轴对称的风筝,其中∠BCD=90°,延长DC、BC分别与AB、AD交于点E、F,点E、F分别为AB、AD的中点,在线段AC和EF处用轻质钢丝做成十字形风筝龙骨,在图3的正方形中画出一种剪拼示意图,并求出相应轻质钢丝的总长度.(说明:题中的拼接都是不重叠无缝隙无剩余)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC. 
(1)求证:∠1=∠2;
(2)连结BE、DE,判断四边形BCDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知∠B=30°,⊙O的半径为12,弧DE的长度为4π. 
(1)求证:DE∥BC;
(2)若AF=CE,求线段BC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2 , y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某篮球运动员去年共参加40场比赛,其中3分球的命中率为0.25,平均每场有12次3分球未投中.
(1)该运动员去年的比赛中共投中多少个3分球?
(2)在其中的一场比赛中,该运动员3分球共出手20次,小亮说,该运动员这场比赛中一定投中了5个3分球,你认为小亮的说法正确吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com