
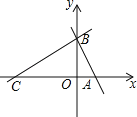
【题目】如图,平面直角坐标系中,直线y=﹣![]() x+
x+![]() 与坐标轴交与点A、B.点C在x轴的负半轴上,且AB:AC=1:2.
与坐标轴交与点A、B.点C在x轴的负半轴上,且AB:AC=1:2.
(1)求A、C两点的坐标;
(2)若点M从点C出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;
(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点,且以AB为边的四边形是菱形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)C(﹣3,0);(2)S=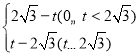 ;(3)存在,满足题意的点Q的坐标为(1,2)或(1,﹣2)或(﹣1,0)
;(3)存在,满足题意的点Q的坐标为(1,2)或(1,﹣2)或(﹣1,0)
【解析】
(1)求出A,B两点的坐标,求出AB=2,则OC可求出,则点C的坐标可求出;
(2)先求出∠ABC=90°,分两种情况考虑:当M在线段BC上;当M在线段BC延长线上;表示出BM,利用三角形面积公式分别表示出S与t的函数关系式即可;
(3)点P是y轴上的点,在坐标平面内存在点Q,使以A、B、P、Q为顶点的四边形是菱形,如图所示,利用菱形的性质,根据AQ与y轴平行或垂直,求出满足题意Q得坐标即可.
解:(1)对于直线y=﹣![]() x+
x+![]() ,
,
当y=0 时,![]() =0,
=0,
解得:x=1,
∴A(1,0),
∴OA=1,
当x=0 时,y=![]() ,
,
∴B(0,![]() ),
),
∴OB=![]() ,
,
∵∠AOB=90°,
∴AB=![]() =
=![]() =2,
=2,
∵AB:AC=1:2,
∴AC=4,
∴OC=3,
∴C(﹣3,0);
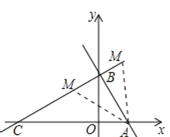
(2)如图所示,
∵![]() ,
,![]() ,
,![]() ,
,
∴∠ABO=30°,
同理:BC=2![]() ,∠OCB=30°,
,∠OCB=30°,
∴∠OBC=60°,
∴∠ABC=90°,
分两种情况考虑:
①若M在线段BC上时,
BC=2![]() ,CM=t,可得BM=BC﹣CM=2
,CM=t,可得BM=BC﹣CM=2![]() ﹣t,
﹣t,
此时S△ABM=![]() BMAB=
BMAB=![]() ×(2
×(2![]() ﹣t)×2=2
﹣t)×2=2![]() ﹣t(0≤t<2
﹣t(0≤t<2![]() );
);
②若M在BC延长线上时,BC=2![]() ,CM=t,
,CM=t,
可得BM=CM﹣BC=t﹣2![]() ,
,
此时S△ABM=![]() BMAB=
BMAB=![]() ×(t﹣2
×(t﹣2![]() )×2=t﹣2
)×2=t﹣2![]() (t≥2
(t≥2![]() );
);
综上所述,S=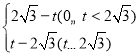 ;
;
(3)存在.若AB是菱形的边,如下图所示,
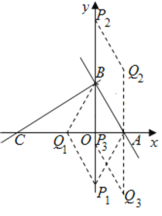
在菱形AP1Q1B中,Q1O=AO=1,所以Q1点的坐标为(﹣1,0),
在菱形ABP2Q2中,AQ2=AB=2,所以Q2点的坐标为(1,2),
在菱形ABP3Q3中,AQ3=AB=2,所以Q3点的坐标为(1,﹣2),
综上,满足题意的点Q的坐标为(1,2)或(1,﹣2)或(﹣1,0).


科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数y=![]() (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y=![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1;2,△OAC与△CBD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1;2,△OAC与△CBD的面积之和为![]() ,则k的值为( )
,则k的值为( )
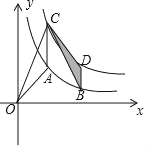
A.2B.3C.4D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某中学一次趣味运动会50米托盘乒乓球接力项目中(即乒乓球放入托盘内,参赛队员用手托住托盘运送乒乓球),初一(1)班和初一(2)班同台竞技,某时刻,1班的小敏和2班的小文分别位于50米赛道的起点![]() 地和终点
地和终点![]() 地,他们同时出发,相向而行,分别以各自的速度匀速直线奔跑,过程中的某时刻,小敏不慎将乒乓球落在
地,他们同时出发,相向而行,分别以各自的速度匀速直线奔跑,过程中的某时刻,小敏不慎将乒乓球落在![]() 地(
地(![]() 、
、![]() 、
、![]() 在同一直线上且乒乓球落在
在同一直线上且乒乓球落在![]() 地后不再移动),第6秒时小敏才发现并迅速掉头以原速去捡乒乓球,捡到球后,小敏将速度提升到小文速度的两倍迅速往
地后不再移动),第6秒时小敏才发现并迅速掉头以原速去捡乒乓球,捡到球后,小敏将速度提升到小文速度的两倍迅速往![]() 地匀速跑去,小敏掉头和捡球的时间忽略不计,如图是两人之间的距离
地匀速跑去,小敏掉头和捡球的时间忽略不计,如图是两人之间的距离![]() (米)与小敏出发的时间
(米)与小敏出发的时间![]() (秒)之间的函数图象,则当小敏到达
(秒)之间的函数图象,则当小敏到达![]() 地时,小文离
地时,小文离![]() 地还有________米.
地还有________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论正确的是( )
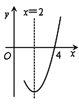
A.当x<2时,y随x增大而增大B.a-b+c<0
C.拋物线过点(-4,0)D.4a+b=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量![]() 与单价
与单价![]() 满足一次函数关系,求出
满足一次函数关系,求出![]() 与
与![]() 的关系式;
的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
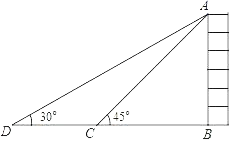
【题目】如图所示,初三数学兴趣小组同学为了测量垂直于水平地面的一座大厦AB的高度,一测量人员在大厦附近C处,测得建筑物顶端A处的仰角大小为45°,随后沿直线BC向前走了60米后到达D处,在D处测得A处的仰角大小为30°,则大厦AB的高度约为多少米?(注:不计测量人员的身高,结果按四舍五入保留整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
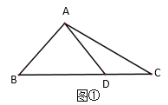
【题目】(问题探究)课堂上老师提出了这样的问题:“如图①,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的一点,
边上的一点,![]() ,求
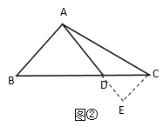
,求![]() 的长”.某同学做了如下的思考:如图②,过点
的长”.某同学做了如下的思考:如图②,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,进而求解,请回答下列问题:
,进而求解,请回答下列问题:
(1)![]() ___________度;
___________度;
(2)求![]() 的长.
的长.
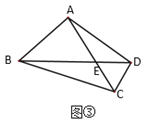
(拓展应用)如图③,在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 相交于点
相交于点![]() ,且
,且![]() ,
,![]() ,则
,则![]() 的长为_____________.
的长为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com