
分析 (1)根据二次函数的性质、绝对值的性质,特殊角三角函数值,根据特殊角三角函数值,可得答案;
(2)根据特殊角三角函数值,可得答案;
(3)根据特殊角三角函数值,可得答案.
解答 解:(1)原式=cot30°-1+1-tan35°+tan35°-cot45°
=$\sqrt{3}$-1;
(2)原式=$\frac{1}{4}$+$\frac{1-2×(\frac{\sqrt{3}}{2})^{2}}{1-2×\frac{\sqrt{3}}{2}×\frac{\sqrt{3}}{2}}$+0=$\frac{1}{4}$+1=$\frac{5}{4}$;
(3)原式=$\frac{2×\frac{\sqrt{3}}{3}}{1-\frac{\sqrt{3}}{3}}$-$\frac{1-\sqrt{3}}{1+\sqrt{3}}$+($\frac{\sqrt{3}}{2}$+$\frac{\sqrt{3}}{2}$)2=1+$\frac{1-2\sqrt{3}+3}{2}$+3=6-$\sqrt{3}$.
点评 本题考查了特殊角三角函数值,熟记特殊角三角函数值是解题关键,注意非零的零次幂等于1.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
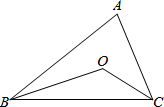 如图,△ABC的∠ABC和∠ACB的平分线交于点O,解答:
如图,△ABC的∠ABC和∠ACB的平分线交于点O,解答:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com