练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在平面直角坐标系xOy中，直线y=﹣x+3交y轴于点A，交反比例函数y= （k＜0）的图象于点D，y= （k＜0）的图象过矩形OABC的顶点B，矩形OABC的面积为4，连接OD．
    （1）求反比例函数y= 的表达式；
    （2）求△AOD的面积．

    【答案】
    （1）解：∵直线y=﹣x+3交y轴于点A，

    ∴点A的坐标为（0，3），即OA=3，

    ∵矩形OABC的面积为4，

    ∴AB= ，

    ∵双曲线在第二象限，

    ∴k=4，

    ∴反比例函数的表达式为y=﹣ ；


    （2）解：解方程组 ，

    得 ， ，

    ∵点D在第二象限，

    ∴点D的坐标为（﹣1，4），

    ∴△AOD的面积= ×3×1= ．


    【解析】（1）根据矩形的面积求出AB，求出反比例函数的解析式；（2）解方程组求出反比例函数与一次函数的交点，确定点D的坐标，根据三角形的面积公式计算即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某林业部门要考察某种幼树在一定条件下的移植成活率，在同样的条件下对这种幼树进行大量移植，并统计成活情况，记录如下（其中频率结果保留小数点后三位）

    移植总数（n）

    10

    50

    270

    400

    750

    1500

    3500

    7000

    9000

    成活数（m）

    8

    47

    235

    369

    662

    1335

    3203

    6335

    8118

    成活的频率

    0.800

    0.940

    0.870

    0.923

    0.883

    0.890

    0.915

    0.905

    0.902

    由此可以估计幼树移植成活的概率为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学活动课上，老师和学生一起去测量学校升旗台上旗杆AB的高度．如图，老师测得升旗台前斜坡FC的坡比为iFC=1：10（即EF：CE=1：10），学生小明站在离升旗台水平距离为35m（即CE=35m）处的C点，测得旗杆顶端B的仰角为α．已知tanα= ，升旗台高AF=1m，小明身高CD=1.6m，请帮小明计算出旗杆AB的高度．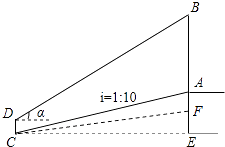

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“元旦”期间，某商场为了吸引顾客购物消费，设计了如图所示的一个转盘，转盘平均分成3份.
    （1）求转动该转盘一次所得的颜色是黄色的概率；
    （2）请用列表法或画树状图的方法来说明转动该转盘两次，两次所得的颜色相同的概率.
    （3）该商场设计了如下两种奖励方案：方案一，转动该转盘一次，若转得的颜色是黄色则可得奖；方案二，转动该转盘两次，若两次转得的颜色相同则可得奖。如果你是顾客，你选择哪种方案比较划算？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在矩形ABCD中，动点E从A出发，沿AB→BC方向运动，当点E到达点C时停止运动，过点E做FE⊥AE，交CD于F点，设点E运动路程为x，FC=y，如图2所表示的是y与x的函数关系的大致图象，当点E在BC上运动时，FC的最大长度是 ，则矩形ABCD的面积是（ ）

    A.
    B.5
    C.6
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD和正方形EFCG的边长分别为3和1，点F，G分别在边BC，CD上，P为AE的中点，连接PG，则PG的长为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一个直角三角形纸片ABO放置在平面直角坐标系中，点 ，点B（0，1），点O（0，0）．P是边AB上的一点（点P不与点A，B重合），沿着OP折叠该纸片，得点A的对应点A'．
    （1）如图①，当点A'在第一象限，且满足A'B⊥OB时，求点A'的坐标；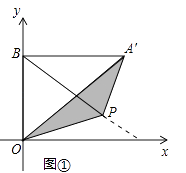

    （2）如图②，当P为AB中点时，求A'B的长；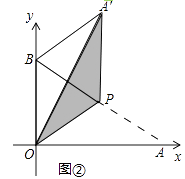

    （3）当∠BPA'=30°时，求点P的坐标（直接写出结果即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况，随机抽查部分学生做了一次问卷调查，要求学生选出自己最喜欢的一个版面，将调查数据进行了整理、绘制成部分统计图如下：

    请根据图中信息，解答下列问题：
    （1）该调查的样本容量为 ， a=%，“第一版”对应扇形的圆心角为°；
    （2）请你补全条形统计图；
    （3）若该校有1000名学生，请你估计全校学生中最喜欢“第三版”的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y= x2+bx+c与x轴交于点A（﹣2，0），交y轴于点B（0， ）．直线y=kx 过点A与y轴交于点C，与抛物线的另一个交点是D．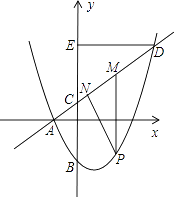

    （1）求抛物线y= x2+bx+c与直线y=kx 的解析式；
    （2）设点P是直线AD下方的抛物线上一动点（不与点A、D重合），过点P作y轴的平行线，交直线AD于点M，作DE⊥y轴于点E．探究：是否存在这样的点P，使四边形PMEC是平行四边形？若存在请求出点P的坐标；若不存在，请说明理由；
    （3）在（2）的条件下，作PN⊥AD于点N，设△PMN的周长为m，点P的横坐标为x，求m与x的函数关系式，并求出m的最大值．

    查看答案和解析>>

    同步练习册答案