
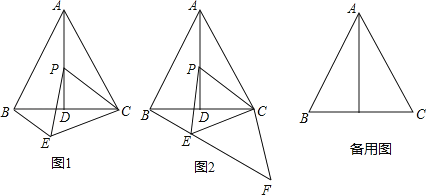
【题目】如图1,等边![]() 边长为6,
边长为6,![]() 是
是![]() 的中线,
的中线,![]() 为线段
为线段![]() (不包括端点
(不包括端点![]() 、
、![]() 上一动点,以
上一动点,以![]() 为一边且在
为一边且在![]() 左下方作如图所示的等边
左下方作如图所示的等边![]() ,连结
,连结![]() .
.
(1)点![]() 在运动过程中,线段
在运动过程中,线段![]() 与
与![]() 始终相等吗?说说你的理由;
始终相等吗?说说你的理由;
(2)若延长![]() 至
至![]() ,使得
,使得![]() ,如图2,问:
,如图2,问:
①求出此时![]() 的长;
的长;
②当点![]() 在线段
在线段![]() 的延长线上时,判断
的延长线上时,判断![]() 的长是否为定值,若是请直接写出
的长是否为定值,若是请直接写出![]() 的长;若不是请简单说明理由.
的长;若不是请简单说明理由.
【答案】(1)![]() ,理由见解析;(2)①
,理由见解析;(2)①![]() ;②定值,8.
;②定值,8.
【解析】
(1)先证明![]() ,然后依据
,然后依据![]() 证明
证明![]() ,由全等三角形的性质可得到
,由全等三角形的性质可得到![]() ;
;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,先依据等腰三角形三线合一的性质求得
,先依据等腰三角形三线合一的性质求得![]() ,然后由
,然后由![]() 可求得
可求得![]() ,依据含
,依据含![]() 直角三角形的性质可求得
直角三角形的性质可求得![]() 的长,从而可求得
的长,从而可求得![]() 的长,然后在
的长,然后在![]() 中依据勾股定理可求得
中依据勾股定理可求得![]() 的长,故此可求得
的长,故此可求得![]() 的长,最后根据
的长,最后根据![]() 求解即可;
求解即可;
(3)首先根据题意画出图形,过点![]() 作
作![]() ,垂足为
,垂足为![]() .先证
.先证![]() ,从而得到
,从而得到![]() ,由含
,由含![]() 直角三角形的性质可求得
直角三角形的性质可求得![]() 的长,依据勾股定理可求得
的长,依据勾股定理可求得![]() 的长,然后由等腰三角形三线合一的性质可得到
的长,然后由等腰三角形三线合一的性质可得到![]() ,故此可求得
,故此可求得![]() 的长.
的长.
(1)![]() .
.
理由如下:
![]() 和
和![]() 均为等边三角形,
均为等边三角形,
![]() ,
,![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() 在
在![]() 和
和![]() 中,
中, ,
,
![]() .
.
![]() ;
;
(2)如图2所示:过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
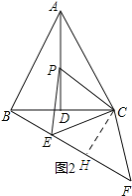
![]() ,
,![]() 是
是![]() 的中线,
的中线,
![]() .
.
![]() 由(1)可知:
由(1)可知:![]() ,
,
![]() ,
,![]() .
.
![]() 在
在![]() 中,
中,![]() ,
,
![]() ,
,![]() .
.
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
![]() ;
;
(3)如图3所示:过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.

![]() 和
和![]() 均为等边三角形,
均为等边三角形,
![]() ,
,![]() ,
,![]() .
.
![]() ,即
,即![]() ,
,
![]() 在
在![]() 和
和![]() 中,
中, ,
,
![]() ,
,
![]() .
.
![]() 在
在![]() 中,
中,![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() .
.
![]() .
.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】对于多项式Ax2bxc(b、c为常数),作如下探究:
(1)不论x取何值,A都是非负数,求b与c满足的条件;
(2)若A是完全平方式,
①当c=9时,b= ;当b=3时,c= ;
②若多项式Bx2dxc与A有公因式,求d的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①b<0;②a+b+c<0;③4a-2b+c<0;④2a-b<0,其中正确的有______.(填代号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是( )

A. ∠B=∠E,BC=EF B. ∠A=∠D,BC=EF
C. ∠A=∠D,∠B=∠E D. BC=EF,AC=DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,AB=AC=2,∠A=90°,D为BC中点,点E,F分别在AB,AC上,且BE=AF,

(1)求证:ED=FD,
(2)求证:DF⊥DE,
(3)求四边形AFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,A(m,0)为 x 轴负半轴上的点,B(0,n)为 y 轴负半轴上的点.
(1)如图,以 A 点为顶点,AB 为腰在第三象限作等腰 Rt△ABC.若已知 m= 2,n= 4,试求 C 点的坐标;
(2)若∠ACB=90°,点 C 的坐标为(4, 4),请在坐标系中画出图形并求 n﹣m 的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (k>0,x>0)的图象与直线y=2x﹣2交于点Q(2,m).
(k>0,x>0)的图象与直线y=2x﹣2交于点Q(2,m).
(1)求m,k的值;
(2)已知点P(a,0)(a>0)是x轴上一动点,过点P作平行于y轴的直线,交直线y=2x﹣2于点M,交函数y=![]() 的图象于点N.
的图象于点N.
①当a=4时,求MN的长;
②若PM>PN,结合图象,直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在笔直的公路![]() 旁有一座山,为方便运输货物现要从公路
旁有一座山,为方便运输货物现要从公路![]() 上的
上的![]() 处开凿隧道修通一条公路到
处开凿隧道修通一条公路到![]() 处,已知点
处,已知点![]() 与公路上的停靠站
与公路上的停靠站![]() 的距离为
的距离为![]() ,与公路上另-停靠站
,与公路上另-停靠站![]() 的距离为
的距离为![]() ,停靠站
,停靠站![]() 之间的距离为
之间的距离为![]() ,且
,且![]()
![]() 求修建的公路
求修建的公路![]() 的长;
的长;
![]() 若公路
若公路![]() 修通后,辆货车从
修通后,辆货车从![]() 处经过
处经过![]() 点到
点到![]() 处的路程是多少?
处的路程是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:
,下列结论: ![]() ;
; ![]() ;
; ![]() ;
; ![]() 若点
若点![]() 、点
、点![]() 、点
、点![]() 在该函数图象上,则
在该函数图象上,则![]() ;
; ![]() 若方程
若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() ,则
,则![]() 其中正确的结论是______.
其中正确的结论是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com