
【题目】在直角坐标系中,A(m,0)为 x 轴负半轴上的点,B(0,n)为 y 轴负半轴上的点.
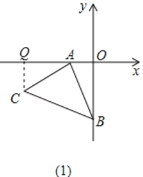
(1)如图,以 A 点为顶点,AB 为腰在第三象限作等腰 Rt△ABC.若已知 m= 2,n= 4,试求 C 点的坐标;
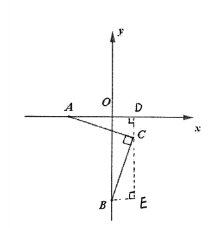
(2)若∠ACB=90°,点 C 的坐标为(4, 4),请在坐标系中画出图形并求 n﹣m 的值.

【答案】(1)C(﹣6,﹣2);(2)画图见解析;-8
【解析】
(1)如图(1)作CQ⊥OA于点Q,通过证明△AQC≌△BOA,即可得到CQ=AO=2,AQ=BO=4,从而求 C 点的坐标;
(2)按题意作图,过C作CD⊥x轴,BE⊥y轴,通过证明△ADC≌△CEB,可得AD=CE,再根据AD=4-m,CE=-4-n,代入即可求出n﹣m 的值.
(1)如图(1)作CQ⊥OA于点Q,
∴∠AQC=∠AOB =90°
∵△ABC是等腰直角三角形,
∴AC=AB,∠CAB=90°,
∴∠ACQ+∠CAQ=90°,∠BAO+∠CAQ=90°
∴∠ACQ=∠BAO,
在△AQC与△BOA中,
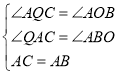 ,
,
∴△AQC≌△BOA,
∴CQ=AO=2,AQ=BO=4.OQ=OA+AQ=6,
∴C(﹣6,﹣2).
(2)如下图所示,过C作CD⊥x轴,BE⊥y轴
∵C的坐标为(4,![]() 4)
4)
∴BE=CD
∵![]()
∴![]()
∴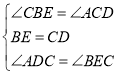
∴△ADC≌△CEB,
∴AD=CE
∵AD=4-m.CE=-4-n
∴4-m=-4-n
∴n-m=-8.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
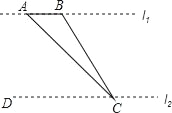
【题目】如图,某数学兴趣小组为了测量河对岸l1的两棵古树A、B之间的距离,他们在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则古树A、B之间的距离为_____m.
查看答案和解析>>
科目:初中数学 来源: 题型:
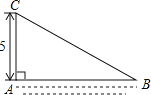
【题目】如图所示,在离水面高度5米的岸上有人用绳子拉船靠岸,开始时绳子BC的长度为13米,此人以每秒0.5米的速度收绳.问:
(1)未开始收绳的时候,图中船B距岸A的长度AB是多少米?
(2)收绳10秒后船向岸边移动了多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传“扫黑除恶”专项行动,社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边,已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的90%,若设白边的宽为x米,则根据题意可列出方程( )

A. 90%×(2+x)(1+x)=2×1 B. 90%×(2+2x)(1+2x)=2×1
C. 90%×(2﹣2x)(1﹣2x)=2×1 D. (2+2x)(1+2x)=2×1×90%
查看答案和解析>>
科目:初中数学 来源: 题型:
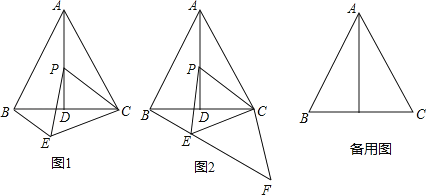
【题目】如图1,等边![]() 边长为6,
边长为6,![]() 是
是![]() 的中线,
的中线,![]() 为线段
为线段![]() (不包括端点
(不包括端点![]() 、
、![]() 上一动点,以
上一动点,以![]() 为一边且在
为一边且在![]() 左下方作如图所示的等边
左下方作如图所示的等边![]() ,连结
,连结![]() .
.
(1)点![]() 在运动过程中,线段
在运动过程中,线段![]() 与
与![]() 始终相等吗?说说你的理由;
始终相等吗?说说你的理由;
(2)若延长![]() 至
至![]() ,使得
,使得![]() ,如图2,问:
,如图2,问:
①求出此时![]() 的长;
的长;
②当点![]() 在线段
在线段![]() 的延长线上时,判断
的延长线上时,判断![]() 的长是否为定值,若是请直接写出
的长是否为定值,若是请直接写出![]() 的长;若不是请简单说明理由.
的长;若不是请简单说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,斜边
中,斜边![]() 的中垂线
的中垂线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() ,
,![]() 于点
于点![]() ,
,![]() 垂直
垂直![]() 的延长线与点
的延长线与点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,现有不列结论:①
,现有不列结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,⑤
,⑤![]() ,其中正确的个数是( )
,其中正确的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
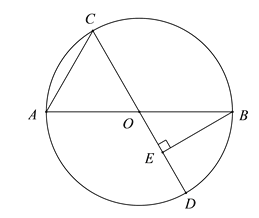
【题目】如图,点C是以AB为直径的⊙O上一动点,过点C作⊙O直径CD,过点B作BE⊥CD于点E.已知AB=6cm,设弦AC的长为xcm,B,E两点间的距离为ycm(当点C与点A或点B重合时,y的值为0).
小冬根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小冬的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
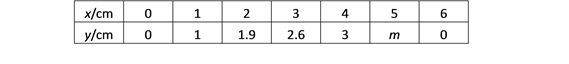
经测量m的值是(保留一位小数).
(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;

(3)在(2)的条件下,当函数图象与直线![]() 相交时(原点除外),∠BAC的度数是_____.
相交时(原点除外),∠BAC的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=x2+(2m﹣1)x﹣2m.
(1)若m=1,抛物线C交x轴于A,B两点,求AB的长;
(2)若一次函数y=kx+mk的图象与抛物线C有唯一公共点,求m的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com