
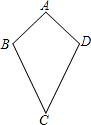
 【问题提出】
【问题提出】分析 【性质】根据图形及定义可以得出结论;【判定】结合图形与筝形的性质,可得出判定定理;【应用】(1)拆分筝形成两个三角形即可得出结论;(2)由直径所对的圆周角为90°能够找到缺失的条件--两个直角;(3)模拟三角形内切圆的画法的步骤即可得出结论.
解答 解:【性质】
结合判定的方法一和图形,即可得出结论:
从边看:有且只有两组邻边分别相等;从对角线看:有且只有一条对角线被另一条对角线垂直平分.
故答案为:两组对边都不平行;有且只有一条对角线被另一条对角线垂直平分.
【判定】
结合性质定理,可得出:方法二:从对角线看:有且只有一条对角线被另一条对角线垂直平分.
结合方法二可知缺少的条件为:AC垂直平分BD于O点,且AO≠CO.
故答案为:有且只有一条对角线被另一条对角线垂直平分;AC垂直平分BD于O点,且AO≠CO.
证明:按照题意,画出图形1.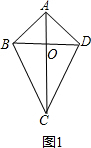
∵AC垂直平分BD,
∴AB=AD,CB=CD.
又∵AB=$\sqrt{A{O}^{2}+B{O}^{2}}$,BC=$\sqrt{B{O}^{2}+C{O}^{2}}$,AO≠CO,
∴AB≠BC,
∴由筝形定义得,四边形ABCD是筝形.
【应用】
(1)筝形面积为对角线乘积的一半;
∵SABCD=S△ABD+S△CBD=$\frac{1}{2}$BD•AO+$\frac{1}{2}$BD•CO=$\frac{1}{2}$BD(AO+CO)=$\frac{1}{2}$BD•AC,
∴筝形面积为对角线乘积的一半.
(2)不一定有,如果∠ABC=∠ADC=90°时,则有外接圆;
∵筝形只有一组对角相等,
∴∠ABC=∠ADC.
又∵AC>BD,
∴若筝形存在外接圆,其圆心为线段AC的中点,
∵B、D点在圆上,
∴∠ABC=∠ADC=90°.
故:不一定有,如果∠ABC=∠ADC=90°时,则有外接圆.
(3)有,作∠A和∠B的角平分线交于一点,过交点作AD的垂线,然后以交点为圆心,以垂线段为半径作圆,即为所求内切圆.
由筝形的性质可得出:$\left\{\begin{array}{l}{AB=AD}\\{BC=DC}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC,
∴∠BAC=∠DAC,∠BCA=∠DCA,
∴CA是∠BAD的角平分线.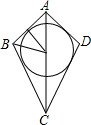
由AC为筝形对称轴可以得知存在内接圆.
点评 本题考查了新概念中的筝形的性质及判定,解题的关键是:读懂题意理清关系,用数学的语言合理的叙述.本题属于中档题型,难度不大,对应以前接触过筝形的同学来说本题不难,对于没接触过的同学来说有点难度,失分点是性质和判定定理的叙述,结合我们学过的知识,平行四边形、长方形和正方形的性质和判定定理,选用合适的数学语言来叙述是得分的关键,此处体现出了数学的严谨性.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 (1)二次函数的图象经过点(4,-3),且当x=3时,函数有最大值-1,求此函数的解析式;
(1)二次函数的图象经过点(4,-3),且当x=3时,函数有最大值-1,求此函数的解析式;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
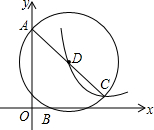 如图,平面直角坐标系中,已知A(0,3),B(1,0),点C在第一象限,⊙D经过点A、B、C三点,AC是⊙O的直径,双曲线y=$\frac{k}{x}$(x>0)经过D、C两点,则k的值是4.
如图,平面直角坐标系中,已知A(0,3),B(1,0),点C在第一象限,⊙D经过点A、B、C三点,AC是⊙O的直径,双曲线y=$\frac{k}{x}$(x>0)经过D、C两点,则k的值是4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
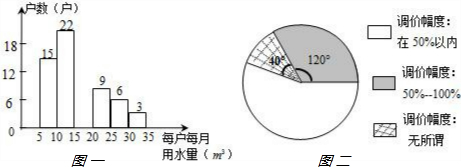
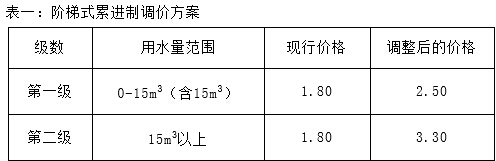
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com