
 (1)如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DAO.
(1)如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DAO.分析 (1)根据菱形的对角线互相平分可得OD=OB,再根据直角三角形斜边上的中线等于斜边的一半可得OH=OB,然后根据等边对等角求出∠OHB=∠OBH,根据两直线平行,内错角相等求出∠OBH=∠ODC,然后根据等角的余角相等证明即可.
(2)首先将二次项系数化为1.然后移项,把常数项移到等号的右边,方程左右两边同时加上一次项系数一半的平方,则左边是完全平方式,右边是常数项,即可直接开方求解.
解答 (1)证明:∵四边形ABCD是菱形,
∴OD=OB,∠COD=90°,
∵DH⊥AB,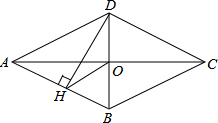
∴OH=$\frac{1}{2}$BD=OB,
∴∠OHB=∠OBH,
又∵AB∥CD,
∴∠OBH=∠ODC,
在Rt△COD中,∠ODC+∠DCO=90°,
在Rt△DHB中,∠DHO+∠OHB=90°,
∴∠DHO=∠DCO,
∵DA=DC,
∴∠DAO=∠DCO,
∴∠DHO=∠DAO;
(2)解:原方程可化为x2-$\frac{1}{6}$x=2,
∴x2-$\frac{1}{6}$x+($\frac{1}{12}$)2=2+($\frac{1}{12}$)2,
配方得(x-$\frac{1}{12}$)2=$\frac{289}{144}$,
∴x-$\frac{1}{12}$=±$\frac{17}{12}$
解得x1=$\frac{3}{2}$,x2=-$\frac{4}{3}$.
点评 (1)本题考查了菱形的对角线互相垂直平分的性质,直角三角形斜边上的中线等于斜边的一半的性质,以及等角的余角相等,熟记各性质并理清图中角度的关系是解题的关键.
(2)本题考查了用配方法解一元二次方程,配方法的一般步骤:①把常数项移到等号的右边;②把二次项的系数化为1;③等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
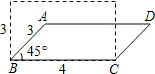 如图,矩形的长和宽分别是4和3,当矩形被“压扁”成内角为45°的平行四边形时,面积大约变成了原来的( )
如图,矩形的长和宽分别是4和3,当矩形被“压扁”成内角为45°的平行四边形时,面积大约变成了原来的( )| A. | 50% | B. | 60% | C. | 70% | D. | 80% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
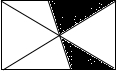 小明把如图所示的矩形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是( )
小明把如图所示的矩形纸板挂在墙上,玩飞镖游戏(每次飞镖均落在纸板上),则飞镖落在阴影区域的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
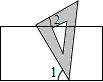 如图,小明把一块含有60°角的直角三角板的两个顶点分别放在矩形的一组对边上,并测得∠1=55°,则∠2的度数是( )
如图,小明把一块含有60°角的直角三角板的两个顶点分别放在矩形的一组对边上,并测得∠1=55°,则∠2的度数是( )| A. | 45° | B. | 27.5° | C. | 30° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
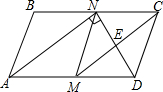 如图,在平行四边形ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点E.
如图,在平行四边形ABCD中,M,N分别是AD,BC的中点,∠AND=90°,连接CM交DN于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
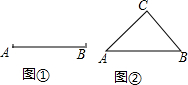 如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com