
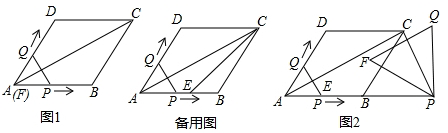
���� ��1��������������˶��ľ��룬�ٳ����ٶȼ������ʱ�䣻
��2���ֵ�0��t��3ʱ����3��t��6ʱ����6��t��9ʱ����9��t��12ʱ������������ֱ�����ص�����������ɣ�
��3���ֽ��㶼��BC��࣬����Ϊ120�㣬���㶼��BC�Ҳ�ʱ�����ǿ���Ϊ30���120�㣻������BC����ʱ������Ϊ150�����������⼴�ɣ�
��� �⣺��1�����ȱߡ�PQF�ı�PQǡ�þ�����Dʱ��
��ͼ1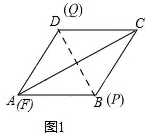
AQ=AD=6��
��t=6��1=6���룩��
���ȱߡ�PQF�ı�QF ǡ�þ�����Eʱ��
��ͼ2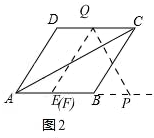
������ABCD�ı߳�Ϊ6����DAB=60�㣬P��Q���ٶȾ�Ϊÿ��1����λ���ȣ�
֪����APQ=60�㣬��QEB=60�㣬
��QE��AD��
�ߵ�E��AB���е㣬
���ʱ��Q��CD���е㣬
����AD+DQ=6+3=9��
����t=9��1=9���룩��
��2��
��ͼ3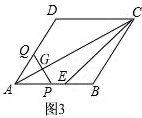
��0��t��3ʱ��
������ABCD�ı߳�Ϊ6����DAB=60�㣬
����PAG=30�㣬
�ߡ�APQ=60�㣬
���AGP=90�㣬
��AP=t������PG=$\frac{1}{2}$t��AG=$\frac{\sqrt{3}}{2}$t��
��S=$\frac{1}{2}$PG��AG=$\frac{\sqrt{3}}{8}{t}^{2}$��
��3��t��6ʱ��
��ͼ4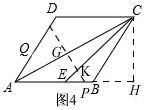
AE=3��AP=t��
��PE=t-3��
����C��AB�Ĵ��ߣ�����ΪH��
������ABCD�ı߳�Ϊ6����DAB=60�㣬
����CH=3$\sqrt{3}$��BH=3��EH=6��
tan��KEB=$\frac{\sqrt{3}}{2}$��
����K��KM��AB��
����KM=$\frac{\sqrt{3}��t-3��}{3}$��
��S��PEK=$\frac{\sqrt{3}��t-3��^{2}}{6}$��
�����QAG=30�㣬
�֡�AQG=60�㣬AQ=t��
�����AGQ=90�㣬
DG=$\frac{1}{2}$t��GQ=$\frac{\sqrt{3}}{2}$t��
��S��AGQ=$\frac{\sqrt{3}}{8}{t}^{2}$��
�ȱ�������APD�����Ϊ��$\frac{\sqrt{3}{t}^{2}}{4}$
��S=$\frac{\sqrt{3}{t}^{2}}{4}$-$\frac{\sqrt{3}}{8}{t}^{2}$-$\frac{\sqrt{3}��t-3��^{2}}{6}$=$-\frac{\sqrt{3}}{24}{t}^{2}+\sqrt{3}t-\frac{3\sqrt{3}}{2}$��
��6��t��9ʱ
��ͼ5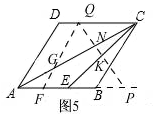
��ǰͬ������S��FQP=$9\sqrt{3}$��
S��GQN=$\frac{\sqrt{3}��12-t��^{2}}{8}$��
S��KEP=$\frac{\sqrt{3}��t-3��^{2}}{6}$��
��S=$9\sqrt{3}$-$\frac{\sqrt{3}��12-t��^{2}}{8}$-$\frac{\sqrt{3}��t-3��^{2}}{6}$=$-\frac{7\sqrt{3}}{24}{t}^{2}+4\sqrt{3}t-\frac{21\sqrt{3}}{2}$��
��9��t��12ʱ��
��ͼ6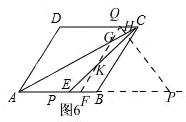
�����S��PQF=$9\sqrt{3}$��
S��QGH=$\frac{\sqrt{3}}{8}��12-t��^{2}$
S��NEP=$\frac{\sqrt{3}}{6}��t-3��^{2}$
S��KEF=$\frac{\sqrt{3}}{14}��t-9��^{2}$��
��S=S��PQF-S��QGH-S��NEP+S��KEF=$9\sqrt{3}$-$\frac{\sqrt{3}}{8}��12-t��^{2}$-$\frac{\sqrt{3}}{6}��t-3��^{2}$+$\frac{\sqrt{3}}{14}��t-9��^{2}$=$\frac{5\sqrt{3}}{24}{t}^{2}-5\sqrt{3}t+30\sqrt{3}$��
��3��
��ʱ����ת��
�٦�=150�㣬��ͼ7
��ʱ�������CNM=��NCM=��APM=��MAP=��DAP=30�㣬
��֤��ACD�ס�APM��
��$\frac{AD}{AM}=\frac{AC}{AP}$��
����AP=12��AC=6$\sqrt{3}$��AD=6��
��ã�AM=$4\sqrt{3}$��
���ԣ�CM=$2\sqrt{3}$��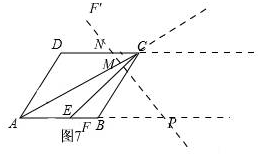
�ڦ�=105�㣬��ͼ8
��ʱ������CM=CN����CMN=��CNM=��APM=75�㣬
��AM=AP=12��
������ABCD�У�AD=CD=6����D=120�㣬
����AC=6$\sqrt{3}$��
���ԣ�CM=12=6$\sqrt{3}$��
�ۦ�=60�㣬��ͼ9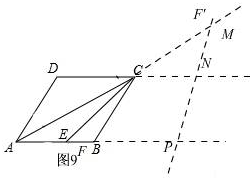
��ʱ�������CMN=��MCN=��ACB=30�㣬
��BC��PM��
��AB=BP=6�ɵã�CM=AC=$6\sqrt{3}$
���ԣ�CM=$6\sqrt{3}$��
�ܦ�=15�㣬��ͼ10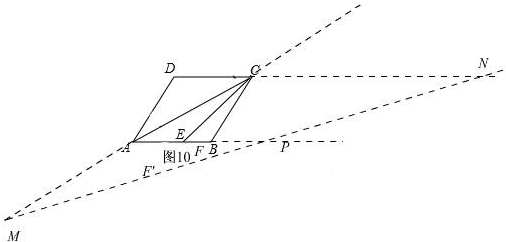
��ʱ�������APM=��M=15�㣬
��AM=AP=12��
���ԣ�CM=AM+AC��
CM=12+$6\sqrt{3}$��
���� ������Ҫ�����ı��ζ����ۺ����⣬������˶�������ö����о��������⣬���ñ�����ʾͼ�����������Ե��������ν��з��������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | -1 | -2 | 3 | -0.5 | 1 | 2 | 0.5 |
| y | 3 | 1.5 | -1 | 6 | -3 | -1.5 | -6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
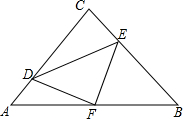 ��ͼ��Rt��ABC�У���ACB=90�㣬AC=BC=8��D��E�DZ�AC��BC���ϵĶ��㣬D��A������C�˶���ͬʱE����ͬ���ٶȴ�C������B�˶���E�˶���Bֹͣ��FΪAB�е㣮
��ͼ��Rt��ABC�У���ACB=90�㣬AC=BC=8��D��E�DZ�AC��BC���ϵĶ��㣬D��A������C�˶���ͬʱE����ͬ���ٶȴ�C������B�˶���E�˶���Bֹͣ��FΪAB�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
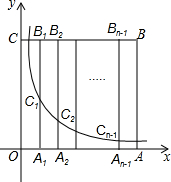 ��ͼ���߳�Ϊn��nΪ����������������OABC�ı�OA��OC���������ϣ���A1��A2������An-1ΪOA��n�ȷֵ㣬��B1��B2��B3����Bn-1ΪCB��n�ȷֵ㣬����A1B1��A2B2��A3B3������An-1Bn-1���ֱ�������y=$\frac{n-8}{x}$��x��0���ཻ�ڵ�C1��C2��C3����Cn-1����B6C6=9A6C6����n��ֵ��20��
��ͼ���߳�Ϊn��nΪ����������������OABC�ı�OA��OC���������ϣ���A1��A2������An-1ΪOA��n�ȷֵ㣬��B1��B2��B3����Bn-1ΪCB��n�ȷֵ㣬����A1B1��A2B2��A3B3������An-1Bn-1���ֱ�������y=$\frac{n-8}{x}$��x��0���ཻ�ڵ�C1��C2��C3����Cn-1����B6C6=9A6C6����n��ֵ��20���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
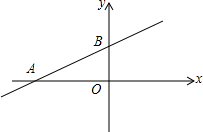 ��ֱ��$y=\frac{1}{2}x+2$�ֱ�x�ᡢy����A��B���㣬��P�Ǹ�ֱ���ϵ�һ�㣬PC��x�ᣬCΪ���㣮
��ֱ��$y=\frac{1}{2}x+2$�ֱ�x�ᡢy����A��B���㣬��P�Ǹ�ֱ���ϵ�һ�㣬PC��x�ᣬCΪ���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
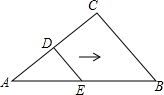 ��ͼ��D��E�ֱ���AC��AB�ϵĵ㣬AD=DC=4��DE=3��DE��BC����C=90�㣬����ADE����AB������ƽ�ƣ�����D����BC��ʱ��ƽ�Ƶľ���Ϊ��������
��ͼ��D��E�ֱ���AC��AB�ϵĵ㣬AD=DC=4��DE=3��DE��BC����C=90�㣬����ADE����AB������ƽ�ƣ�����D����BC��ʱ��ƽ�Ƶľ���Ϊ��������| A�� | 3 | B�� | 4 | C�� | 5 | D�� | 6 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com