
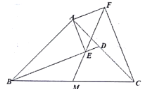
【题目】如图所示,![]() 是等腰直角三角形,其中
是等腰直角三角形,其中![]() ,
,![]() 是
是![]() 边上的一点,连接
边上的一点,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于
于![]() 点.若四边形
点.若四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的面积为__________.
的面积为__________.
【答案】8
【解析】
连接EC,过点B作BH⊥BE交FM的延长线于点H,由“SAS”可证△BAE≌△CAF,可得BE=CF,∠AEB=∠AFC=90°,S△ABE=S△ACF,通过证明△BMH≌△CMF,可得BM=CM,由中线的性质可得S△BME=S△MCE,即可求解.
解:如图,连接EC,过点B作BH⊥BE交FM的延长线于点H,
∵AF⊥AE,AF=AE
∴∠EAF=90°,∠AEF=∠AFE=45°,
∵∠BAC=90°
∴∠BAC=∠EAF,
∴∠BAE=∠CAF,
∵△ABC是等腰直角三角形,
∴AB=AC,∠ABC=45°,
在△BAE和△CAF中
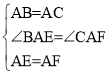
∴△BAE≌△CAF(SAS),
∴BE=CF,∠AEB=∠AFC=90°,S△ABE=S△ACF,
∴∠EAF+∠AFC=180°,
∴AE∥CF,
∴S△CEF=S△CEF=S△ABE,
∵∠AEF=∠AFE=45°,∠AEB=∠AFC=90°,
∴∠BEH=45°,∠CFE=45°,
∵BH⊥BE,
∴∠BEH=∠BHE=45°,
∴BE=EH=CF,且∠BHE=∠CFE=45°,∠BMH=∠CMF,
∴△BMH≌△CMF(AAS)
∴BM=CM,
∴S△BME=S△MCE,
∴S△BME+S△ABE=S△CME+S△CEF,
∴S四边形ABME=S△CMF=8,
故答案为8.



科目:初中数学 来源: 题型:
【题目】如图1,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、l1于点D. E(点A. E位于点B的两侧),满足BP=BE,连接AP、CE.
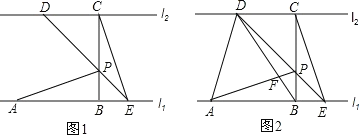
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F. 如图2.
①当![]() =2时,求证:AP⊥BD;
=2时,求证:AP⊥BD;
②当![]() =n(n>1)时,设△DAP的面积为S1,△EPC的面积为S2,求
=n(n>1)时,设△DAP的面积为S1,△EPC的面积为S2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB 是⊙M 的直径,BC 是⊙M 的切线,切点为 B,C 是 BC 上(除 B 点外)的任意一点,连接 CM 交⊙M 于点 G,过点 C 作 DC⊥BC 交 BG 的 延长线于点 D,连接 AG 并延长交 BC 于点 E.
(1)求证:△ABE∽△BCD;
(2)若 MB=BE=1,求 CD 的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b,c是△ABC的三条边,关于x的方程![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景介绍)勾股定理是几何学中的明珠,充满着魅力.千百年来,人们对它的证明趋之若骛,其中有著名的数学家,也有业余数学爱好者.向常春在1994年构造发现了一个新的证法.
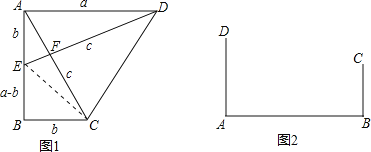
(小试牛刀)把两个全等的直角三角形如图1放置,其三边长分别为a、b、c.显然,∠DAB=∠B=90°,AC⊥DE.请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再探究这三个图形面积之间的关系,可得到勾股定理:
S梯形ABCD= ,
S△EBC= ,
S四边形AECD= ,
则它们满足的关系式为 ,经化简,可得到勾股定理.
(知识运用)(1)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=25千米,BC=16千米,则两个村庄的距离为 千米(直接填空);
(2)在(1)的背景下,若AB=40千米,AD=24千米,BC=16千米,要在AB上建造一个供应站P,使得PC=PD,请用尺规作图在图2中作出P点的位置并求出AP的距离.
(知识迁移)借助上面的思考过程与几何模型,求代数式![]() 最小值(0<x<16)
最小值(0<x<16)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的电脑,已知购买一台A型电脑需0.6万元,购买一台B型电脑需0.4万元,该公司准备投入资金y万元,全部用于购进35台这两种型号的电脑,设购进A型电脑x台.
(1)求y关于x的函数解析式;
(2)若购进B型电脑的数量不超过A型电脑数量的2倍,则该公司至少需要投入资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 延长线上的一点,点
延长线上的一点,点![]() 是
是![]() 的中点。
的中点。

(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法)。
①作![]() 的平分线
的平分线![]() . ②连接
. ②连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
(2)猜想与证明:试猜想![]() 与
与![]() 有怎样的关系,并说明理由。
有怎样的关系,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路MN和公路PQ在点O处交汇,∠QON=30°,公路PQ上A处距O点240米,如果火车行驶时,周围200米以内会受到噪音的影响,那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,求A处受噪音影响的时间。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com