
【题目】甲、乙两位同学本学期11次考试的测试成绩如下:
甲 | 98 | 100 | 100 | 90 | 96 | 91 | 89 | 99 | 100 | 100 | 93 |
乙 | 98 | 99 | 96 | 94 | 95 | 92 | 92 | 98 | 96 | 99 | 97 |
(1) 他们的平均成绩和方差各是多少?
(2) 分析他们的成绩各有什么特点?
(3) 现要从两人中选一人参加比赛,历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,你认为应选谁参加这次比赛?为什么?
【答案】(1)![]() 甲
甲![]() (分),
(分),![]() 乙
乙![]() (分);S2甲
(分);S2甲 ![]() S2乙
S2乙 ![]()
(2)由以上所求得出:两人平均成绩相同,甲的标准差大于乙的标准差,故甲的成绩不稳定;
(3)应选甲谁参加这项竞赛.
【解析】
(1)根据平均数的定义进而求出;利用方差的公式分别求得甲、乙两人的方差;
(2)利用标准差的意义进而分析得出即可;
(3)利用达到98分以上才可能进入决赛,结合两人超过98分的次数即可得出答案.
(1)![]() 甲
甲![]() (分),
(分),
![]() 乙
乙![]() (分);
(分);
S2甲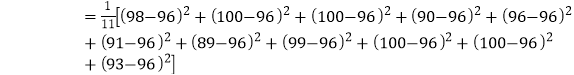
![]()
![]()
S2乙![]()
![]()
![]()
(2)由以上所求得出:两人平均成绩相同,甲的标准差大于乙的标准差,故甲的成绩不稳定;
(3)∵历届比赛成绩表明,平时成绩达到98分以上才可能进入决赛,甲的成绩有6次超过98分,乙的成绩有4次超过98分,
∴应选甲谁参加这项竞赛.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】先阅读,再回答问题:如果x1、x2是关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根,那么x1+x2 , x1x2与系数a、b、c的关系是:x1+x2= ![]() ,
, ![]() ,例如:若x1、x2是方程2x2﹣x﹣1=0的两个根,则x1+x2=﹣
,例如:若x1、x2是方程2x2﹣x﹣1=0的两个根,则x1+x2=﹣ ![]() =
= ![]()
![]() ,x1x2=
,x1x2= ![]() .若x1、x2是方程2x2+x﹣3=0的两个根.
.若x1、x2是方程2x2+x﹣3=0的两个根.
(1)求x1+x2 , x1x2;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,AE∥CD,CE∥AB,连接DE交AC于点O.
(1)证明:四边形ADCE为菱形;
(2)证明:DE=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与计算:请阅读以下材料,并完成相应的任务.
斐波那契(约1170﹣1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用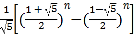 表示(其中,n≥1).这是用无理数表示有理数的一个范例.
表示(其中,n≥1).这是用无理数表示有理数的一个范例.

任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=ADAB;④ABCD=ADCB,能满足△ADC与△ACB相似的条件是( )

A.①、②、③ B.①、③、④ C.②、③、④ D.①、②、④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=∠2,∠3=∠4,则下面结论中错误的是( )

A. △ADC≌△BCD B. △ABD≌△BAC C. △AOB≌△COD D. △AOD≌△BOC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D.求证:AD=BC
证明:∵AB=AC
∴∠ABC=∠C ( )
∵∠A=36°
又∵∠A+∠ABC+∠C=180° ( )
∴∠ABC= °
∵BD平分∠ABC
∴∠1=∠2= °
∴∠C=∠ =72°
∴AD= ,BC= ( )
∴AD=BC

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.
(1)说明△ADE≌△CFE;
(2)判断线段AB、CF、BD之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋中有4个完全相同的小球,它们的标号分别为1,2,3,4,从中随机摸出一个小球记下标号后放回,再从中随机摸出一个小球,求两次摸出的小球的标号之和大于4的概率?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com