
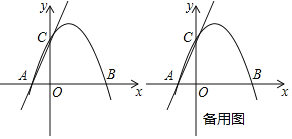
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=2x+b分别交x,y轴于点A、C,抛物线y=ax2+x+4经过A、C两点,交x轴于另外一点B.
(1)求抛物线的解析式;
(2)点P在第一象限内抛物线上,连接PB、PC,作平行四边形PBDC,DE⊥y轴于点E,设点P 的横坐标为t,线段DE的长度为d,求d与t之间的函数关系式.
(3)在(2)的条件下,延长BD交直线AC与点F,连接OF,若∠AFO=∠BFO,求点P的坐标.
【答案】(1)y=-![]() x2+x+4.(2)d =4-t(0<t<4).(3)点P坐标为(
x2+x+4.(2)d =4-t(0<t<4).(3)点P坐标为(![]() ,
,![]() ).
).
【解析】
(1)利用待定系数法即可解决问题.
(2)如图1中,设P(t,-![]() x2+x+4),D(x,y).根据平行四边形的性质对角线互相平分,利用中点坐标公式,列出方程即可解决问题.
x2+x+4),D(x,y).根据平行四边形的性质对角线互相平分,利用中点坐标公式,列出方程即可解决问题.
(3)如图2中,作OM⊥AC于M,ON⊥BF于N,NE⊥OB于E.先求出点N的坐标,求出直线NB的解析式,再求出直线PC的解析式,解方程组即可解决问题.
(1)对于抛物线y=ax2+x+4,令x=0,得y=4,
∴C(0,4),把C(0,4),代入y=2x+b中,得b=4,
∴直线解析式为y=2x+4,令Y=0,得x=-2,
∴A(-2,0),把A(-2,0)代入y=ax2+x+4,得a=-![]() ,
,
∴抛物线的解析式为y=-![]() x2+x+4.
x2+x+4.
(2)如图1中,设P(t,-![]() x2+x+4),D(x,y).
x2+x+4),D(x,y).

∵C(0,4),B(4,0),四边形CPBD是平行四边形,
∴![]() ,x=4-t,
,x=4-t,
∴d=DE=x=4-t(0<t<4).
(3)如图2中,作OM⊥AC于M,ON⊥BF于N,NE⊥OB于E.
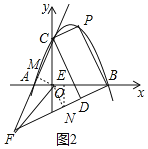
∵∠OFA=∠OFB,OM⊥FC,ON⊥FB,
∴OM=ON,
∵![]() OAOC=
OAOC=![]() ACOM,OA=2,OC=4,AC=
ACOM,OA=2,OC=4,AC=![]() ,
,
∴ON=OM=![]() ,
,
∵BN=![]() ,
,
∵![]() ONBN=
ONBN=![]() OBEN,
OBEN,
∴EN=![]() ,OE=
,OE=![]() ,
,
∴N(![]() ,-
,-![]() ),
),
设直线BN的解析式为y=kx+b,则有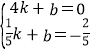 ,解得
,解得  ,
,
∵PC∥BN,
∴直线PC的解析式为y=![]() x+4,
x+4,
由 ,解得
,解得![]() 或
或 ,
,
∴点P坐标为(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
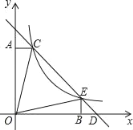
【题目】如图,直线y=﹣x+b与反比例函数y=![]() (k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACO=S△BEO;④S△CEO=15;⑤点D的坐标为(5,0).其中正确的是( )
(k≠0)的图象的一支交于C(1,4),E两点,CA⊥y轴于点A,EB⊥x轴于点B,则以下结论:①k的值为4;②△BED是等腰直角三角形;③S△ACO=S△BEO;④S△CEO=15;⑤点D的坐标为(5,0).其中正确的是( )
A. ①②③B. ①②③④C. ②③④⑤D. ①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
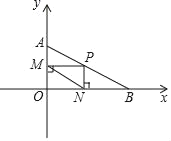
【题目】如图,已知在平面直角坐标系中有两点A(0,1),B(![]() ,0),动点P在线段AB上运动,过点P作y轴的垂线,垂足为点M,作x轴的垂线,垂足为点N,连接MN,则线段MN的最小值为( )
,0),动点P在线段AB上运动,过点P作y轴的垂线,垂足为点M,作x轴的垂线,垂足为点N,连接MN,则线段MN的最小值为( )
A. 1B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三一班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲队 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙队 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是_________分,乙队成绩的众数是_________分;
(2)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是_________队;
(3)测试结果中,乙队获满分的四名同学相当优秀,他们是三名男生、一名女生,现准备从这四名同学中随机抽取两人参加学校组织的经典诵读比赛,用树状图或列表法求恰好抽中一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
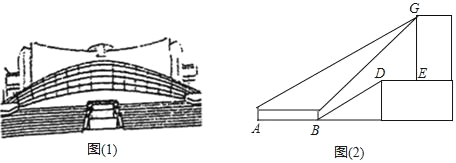
【题目】如图(1)是重庆中国三峡博物馆,又名重庆博物馆,中央地方共建国家级博物馆图(2)是侧面示意图.某校数学兴趣小组的同学要测量三峡博物馆的高GE.如(2),小杰身高为1.6米,小杰在A处测得博物馆楼顶G点的仰角为27°,前进12米到达B处测得博物馆楼顶G点的仰角为39°,斜坡BD的坡i=1:2.4,BD长度是13米,GE⊥DE,A、B、D、E、G在同一平面内,则博物馆高度GE约为_____米.(结果精确到1米,参考数据tan27°≈0.50,tan39°≈0.80)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有24个班,共1 000名学生,他们参加了一次数学测试.学校统计了所有学生的成绩,得到下列统计图.

(1)求该校九年级学生本次数学测试成绩的平均数;
(2)下列关于本次数学测试说法正确的是( )
A.九年级学生成绩的众数与平均数相等
B.九年级学生成绩的中位数与平均数相等
C.随机抽取一个班,该班学生成绩的平均数等于九年级学生成绩的平均数
D.随机抽取300名学生,可以用他们成绩的平均数估计九年级学生成绩的平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
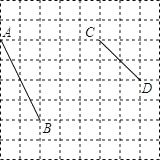
【题目】如图,在小正方形的边长均为1的方格纸中,有线段![]() 和线段
和线段![]() ,点
,点![]() 均在小正方形的顶点上.
均在小正方形的顶点上.
(1)在方格纸中画出以![]() 为斜边的直角三角形
为斜边的直角三角形![]() ,点E在小正方形的顶点上,且
,点E在小正方形的顶点上,且![]() 的面积为5;
的面积为5;
(2)在方格纸中画出以![]() 为一边的
为一边的![]() ,点
,点![]() 在小正方形的顶点上,
在小正方形的顶点上,![]() 的面积为4,射线
的面积为4,射线![]() 与射线
与射线![]() 交于点
交于点![]() ,且
,且![]() ,连接
,连接![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com