
【题目】如图,在半径为2的⊙O中,弦AB长为2.

(1)求点O到AB的距离.
(2)若点C为⊙O上一点(不与点A,B重合),求∠BCA的度数.
【答案】(1)点O到AB的距离为![]() ;(2)∠BCA的度数为30°或150°.
;(2)∠BCA的度数为30°或150°.
【解析】
试题分析:(1)过点O作OC⊥AB于点C,证出△OAB是等边三角形,继而求得∠AOB的度数,然后由三角函数的性质,求得点O到AB的距离;
(2)证出△ABO是等边三角形得出∠AOB=60°. 再分两种情况:点C在优弧![]() 上,则∠BCA=30°;点C在劣弧
上,则∠BCA=30°;点C在劣弧![]() 上,则∠BCA=
上,则∠BCA=![]() (360°﹣∠AOB)=150°;即可得出结果.
(360°﹣∠AOB)=150°;即可得出结果.
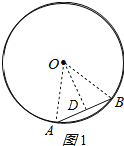
解:(1)过点O作OD⊥AB于点D,连接AO,BO.如图1所示:
∵OD⊥AB且过圆心,AB=2,
∴AD=![]() AB=1,∠ADO=90°,
AB=1,∠ADO=90°,
在Rt△ADO中,∠ADO=90°,AO=2,AD=1,
∴OD=![]() =
=![]() .
.
即点O到AB的距离为![]() .
.
(2)如图2所示:
∵AO=BO=2,AB=2,
∴△ABO是等边三角形,
∴∠AOB=60°.
若点C在优弧![]() 上,则∠BCA=30°;
上,则∠BCA=30°;
若点C在劣弧![]() 上,则∠BCA=
上,则∠BCA=![]() (360°﹣∠AOB)=150°;
(360°﹣∠AOB)=150°;
综上所述:∠BCA的度数为30°或150°.
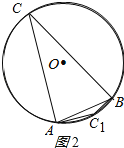


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】分析探索题:细心观察如图,认真分析各式,然后解答问题.
OA22=(![]() )2+1=2 S1=
)2+1=2 S1=![]() ;
;
OA32=(![]() )2+1=3 S2=
)2+1=3 S2=![]() ;
;
OA42=(![]() )2+1=4 S3=
)2+1=4 S3=![]() …
…
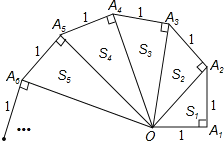
(1)请用含有n(n为正整数)的等式Sn= ;
(2)推算出OA10= .
(3)求出 S12+S22+S32+…+S102的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣2x﹣3.
(1)该二次函数图象的对称轴为 ;
(2)判断该函数与x轴交点的个数,并说明理由;
(3)下列说法正确的是 (填写所有正确说法的序号)
①顶点坐标为(1,﹣4);
②当y>0时,﹣1<x<3;
③在同一平面直角坐标系内,该函数图象与函数y=﹣x2+2x+3的图象关于x轴对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举办了一次以“我的中国梦”为主题的演讲比赛,最后确定7名同学参加决赛,他们的决赛成绩各不相同,其中李华已经知道自己的成绩,但能否进前四名,他还必须清楚这七名同学成绩的( )
A.众数 B.平均数 C.中位数 D.方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com