
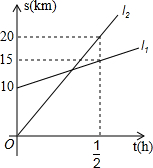
 如图,小王驾驶汽车从甲地开往乙地,同时,小张骑自行车在小王前面10km处,也在向乙地行驶,此图表示小王、小张距甲地的距离s(km)与时间(t)h之间的关系,观察图象并回答下列问题:
如图,小王驾驶汽车从甲地开往乙地,同时,小张骑自行车在小王前面10km处,也在向乙地行驶,此图表示小王、小张距甲地的距离s(km)与时间(t)h之间的关系,观察图象并回答下列问题:分析 (1)由于小张骑自行车在小王前面10km处,不难看出l1表示的是小张距甲地的距离与时间的关系;
(2)由图象知$\frac{1}{2}$时小张骑行了(15-10)千米,小王行驶20千米,不难计算出他们各自的速度;
(3)求出l1、l2的直线解析式,列方程即可求解.
解答 解:(1)根据题意由图象可以看出,l1表示的是小张距甲地的距离与时间的关系;
(2)由图象知$\frac{1}{2}$时小张骑行了(15-10)千米,小王行驶20千米,
∴小张的速度:5÷$\frac{1}{2}$=10千米/时,小张的速度:20÷$\frac{1}{2}$=40千米/时;
(3)由图象知,l1过(0,10)和($\frac{1}{2}$,15)
设l1的直线解析式为:y1=kx+b,
则$\left\{\begin{array}{l}{b=10}\\{\frac{1}{2}k+b=15}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=10}\\{b=10}\end{array}\right.$
∴y1=10x+10,
由图象知l2过原点和($\frac{1}{2}$,20)
设l2的直线解析式为:y2=kx,则20=$\frac{1}{2}$k,
解得:k=40,
∴y2=40x.
当小王追上小张时,即10x+10=40x,
解得x=$\frac{1}{3}$h,
y2=40×$\frac{1}{3}$=$\frac{40}{3}$千米.
故出发$\frac{1}{3}$小时后小王追上小张,此时他们距甲地距离为$\frac{40}{3}$千米.
点评 本题考查了一次函数的图象和实际应用,根据横纵坐标表示的意义,读懂题意,是解决问题的关键.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
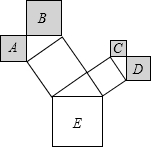 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是2、4、1、2,则正方形E的面积是( )
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是2、4、1、2,则正方形E的面积是( )| A. | 36 | B. | 25 | C. | 18 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
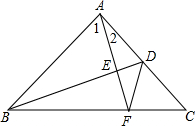 如图所示,在△ABC中,AB=AC,∠BAC=90°,D是AC的中点,AF⊥BD于点E,交BC于点F,连接DF.求证:∠ADB=∠CDF.
如图所示,在△ABC中,AB=AC,∠BAC=90°,D是AC的中点,AF⊥BD于点E,交BC于点F,连接DF.求证:∠ADB=∠CDF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
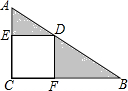 如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=3,DB=4,求阴影部分的面积.
如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=3,DB=4,求阴影部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
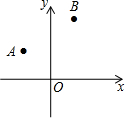 如图,在平面直角坐标系中,点A、B的坐标分别为(-1,2)、(1,4),欲在x轴上找一点P,使PA+PB最短,则点P的坐标为(-$\frac{1}{3}$,0).
如图,在平面直角坐标系中,点A、B的坐标分别为(-1,2)、(1,4),欲在x轴上找一点P,使PA+PB最短,则点P的坐标为(-$\frac{1}{3}$,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com