
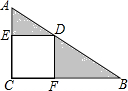
 如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=3,DB=4,求阴影部分的面积.
如图所示,在直角三角形ABC中,∠C=90°,四边形ECFD为正方形,若AD=3,DB=4,求阴影部分的面积.分析 根据正方形的性质得DE=DF,∠EDF=∠DFC=∠DEC=90°,则将△AED绕D点按逆时针方向旋转90°,得到△A1FD,根据旋转的性质得∠ADA′=90°,∠DEA=∠DFA′=90°,则可判断点A′在CF上,所以DA′=DA=3,然后利用阴影部分的面积等于Rt△DA′B的面积求解.
解答 解: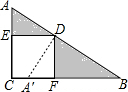 ∵四边形ECFD为正方形,
∵四边形ECFD为正方形,
∴DE=DF,∠EDF=∠DFC=∠DEC=90°,
∴将△AED绕D点按逆时针方向旋转90°,得到△A1FD,如图,
∴∠ADA′=90°,∠DEA=∠DFA′=90°,
∴点A′在CF上,DA′=DA=3,
∴S△DEA=S△DFA′,
∴阴影部分的面积=S△DA′B=$\frac{1}{2}$×3×4=6.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的判定与性质.通过旋转把阴影部分构造成规则的图形是解决此题的关键.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:解答题
| 年级 | 七年级 | 八年级 | 九年级 |
| 学生人数 | 850 | 680 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
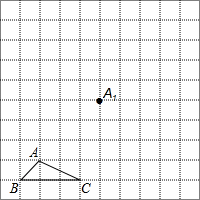 如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
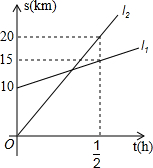 如图,小王驾驶汽车从甲地开往乙地,同时,小张骑自行车在小王前面10km处,也在向乙地行驶,此图表示小王、小张距甲地的距离s(km)与时间(t)h之间的关系,观察图象并回答下列问题:
如图,小王驾驶汽车从甲地开往乙地,同时,小张骑自行车在小王前面10km处,也在向乙地行驶,此图表示小王、小张距甲地的距离s(km)与时间(t)h之间的关系,观察图象并回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
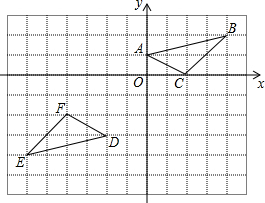 如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为( )
如图,在平面直角坐标系中,将△ABC绕点P旋转180°得到△DEF,则点P的坐标为( )| A. | (-1,0) | B. | (-1,-1) | C. | (-2,-1) | D. | (-2,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com