
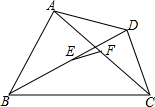
 如图,在四边形ABCD中,AB>CD,E,F分别是对角线BD,AC的中点,求证:$\frac{1}{2}$(AB+CD)>EF.
如图,在四边形ABCD中,AB>CD,E,F分别是对角线BD,AC的中点,求证:$\frac{1}{2}$(AB+CD)>EF. 分析 设BC中点为G,连接EG、FG. 由中位线的性质得EG=$\frac{1}{2}$DC,FG=$\frac{1}{2}$AB,再根据三角形的三边关系可得EF<EG+FG,再利用等量代换可得EF<$\frac{1}{2}$(AB+CD).
解答 证明:设BC中点为G,连接EG、FG.
∵点E、F分别为四边形ABCD的对角线AC、BD的中点,
∴EG=$\frac{1}{2}$DC,FG=$\frac{1}{2}$AB,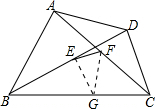
∵在△EFG中,EF<EG+FG,
∴EF<$\frac{1}{2}$(AB+CD),
即$\frac{1}{2}$(AB+CD)>EF.
点评 此题主要考查了三角形中位线的性质以及三角形的三边关系,解题的关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:解答题
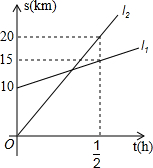 如图,小王驾驶汽车从甲地开往乙地,同时,小张骑自行车在小王前面10km处,也在向乙地行驶,此图表示小王、小张距甲地的距离s(km)与时间(t)h之间的关系,观察图象并回答下列问题:
如图,小王驾驶汽车从甲地开往乙地,同时,小张骑自行车在小王前面10km处,也在向乙地行驶,此图表示小王、小张距甲地的距离s(km)与时间(t)h之间的关系,观察图象并回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
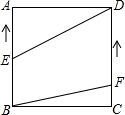 如图,正方形ABCD的边长为6cm,动点E由B向A以2cm/s的速度移动,动点F由C向D以1cm/s的速度移动,E,F分别由B,C同时出发,问几秒钟后四边形BFDE是平行四边形?
如图,正方形ABCD的边长为6cm,动点E由B向A以2cm/s的速度移动,动点F由C向D以1cm/s的速度移动,E,F分别由B,C同时出发,问几秒钟后四边形BFDE是平行四边形?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
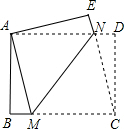 如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,折叠后再展开为矩形ABCD,连结CN.若△CDN的面积与△CMN的面积比为1:4,则$\frac{MN}{BM}$的值为2$\sqrt{6}$.
如图,在矩形ABCD中,AD>AB,将矩形ABCD折叠,使点C与点A重合,折痕为MN,折叠后再展开为矩形ABCD,连结CN.若△CDN的面积与△CMN的面积比为1:4,则$\frac{MN}{BM}$的值为2$\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com