
分析 设AC=x,BC=y,根据S△ABC=$\frac{1}{2}$BC•AC•sinC=$\frac{1}{2}$(AB+AC+BC)r得到r=$\frac{\frac{\sqrt{3}}{2}xy}{x+y+\sqrt{3}}$①在直角三角形CFO中,根据三角函数和切线长定理得到CF=$\sqrt{3}$r=$\frac{1}{2}$(x+y-$\sqrt{3}$)于是得到x+y=2$\sqrt{3}$r+$\sqrt{3}$,x=2$\sqrt{3}$r+$\sqrt{3}$-y代入①,整理得到关于y的一元二次方程$\sqrt{3}$y2-3(2r+1)y+(4$\sqrt{3}$r2+4$\sqrt{3}$r)=0根据△≥0得到4r2+4r-3≥0即可得到结果.
解答 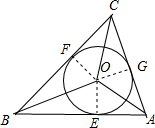 解:如图,设⊙O与△ABC的边相切于E,Q,F,连接OE,OF,OG,
解:如图,设⊙O与△ABC的边相切于E,Q,F,连接OE,OF,OG,
设AC=x,BC=y,
∵S△ABC=$\frac{1}{2}$BC•AC•sinC=$\frac{1}{2}$(AB+AC+BC)r
代入数据得到r=$\frac{\frac{\sqrt{3}}{2}xy}{x+y+\sqrt{3}}$①
又∵在直角三角形CFO中,CF=$\sqrt{3}$r=$\frac{1}{2}$(x+y-$\sqrt{3}$)
∴x+y=2$\sqrt{3}$r+$\sqrt{3}$,∴x=2$\sqrt{3}$r+$\sqrt{3}$-y
代入①,整理得到关于y的一元二次方程$\sqrt{3}$y2-3(2r+1)y+(4$\sqrt{3}$r2+4$\sqrt{3}$r)=0
∵△≥0
得到4r2+4r-3≥0
解得:-$\frac{3}{2}$≤r≤$\frac{1}{2}$
结合题意只能是0<r≤$\frac{1}{2}$,
故答案为0<r≤$\frac{1}{2}$.
点评 本题考查了三角形的内切圆和内心,三角形的面积公式,切线的性质,根据题意画出图形是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
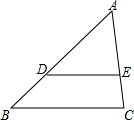 如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )
如图,D、E分别是△ABC的边AB、AC上的点,DE∥BC,且$\frac{AD}{DB}$=2,则△ADE与四边形DBCE的面积比为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{b}>\frac{a+c}{b+c}$ | B. | $\frac{a}{b}<\frac{a+c}{b+c}$ | C. | $\frac{a}{b}=\frac{a+c}{b+c}$ | D. | 前三种均有可能 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com