
【题目】某水产品养殖企业为指导该企业某种产品的养殖和销售,对历年市场行情和水产品的养殖情况进行了调查.调查发现这种水产品的每千克售价![]() (元)与销售月份
(元)与销售月份![]() (月)满足关系式
(月)满足关系式![]() +36,而其每千克成本
+36,而其每千克成本![]() (元)与销售月份
(元)与销售月份![]() (月)满足的函数关系如图所示:
(月)满足的函数关系如图所示:
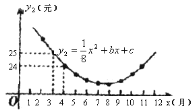
(1)试确定![]() 、
、![]() 的值;
的值;
(2)求出这种水产品每千克的利润![]() (元)与销售月份
(元)与销售月份![]() (月)之间的函数关系式;
(月)之间的函数关系式;
(3)几月份出售这种水产品每千克利润最大?最大利润是多少?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】对于给定的![]() ,我们给出如下定义:若点M是边
,我们给出如下定义:若点M是边![]() 上的一个定点,且以M为圆心的半圆上的所有点都在
上的一个定点,且以M为圆心的半圆上的所有点都在![]() 的内部或边上,则称这样的半圆为
的内部或边上,则称这样的半圆为![]() 边上的点M关于
边上的点M关于![]() 的内半圆,并将半径最大的内半圆称为点M关于
的内半圆,并将半径最大的内半圆称为点M关于![]() 的最大内半圆.若点M是边
的最大内半圆.若点M是边![]() 上的一个动点(M不与B,C重合),则在所有的点M关于
上的一个动点(M不与B,C重合),则在所有的点M关于![]() 的最大内半圆中,将半径最大的内半圆称为
的最大内半圆中,将半径最大的内半圆称为![]() 关于
关于![]() 的内半圆.
的内半圆.
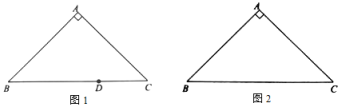
(1)在![]() 中,
中,![]() ,
,![]() ,
,
①如图1,点D在边![]() 上,且
上,且![]() ,直接写出点D关于
,直接写出点D关于![]() 的最大内半圆的半径长;
的最大内半圆的半径长;
②如图2,画出![]() 关于
关于![]() 的内半圆,并直接写出它的半径长;
的内半圆,并直接写出它的半径长;
(2)在平面直角坐标系![]() 中,点E的坐标为
中,点E的坐标为![]() ,点P在直线
,点P在直线![]() 上运动(P不与O重合),将
上运动(P不与O重合),将![]() 关于
关于![]() 的内半圆半径记为R,当
的内半圆半径记为R,当![]() 时,求点P的横坐标t的取值范围.
时,求点P的横坐标t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,且满足
,且满足![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
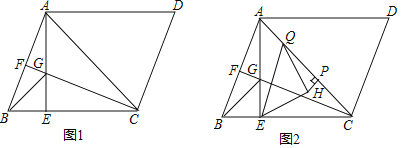
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的长度;
的长度;
(2)如图2取![]() 上一点
上一点![]() ,连接
,连接![]() ,在
,在![]() 内取一点
内取一点![]() ,连接
,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,若
,若![]() ,
,![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
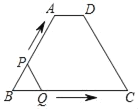
【题目】如图,在四边形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=2,BC=8,点P从点B出发沿折线BA﹣AD﹣DC匀速运动,同时,点Q从点B出发沿折线BC﹣CD匀速运动,点P与点Q的速度相同,当二者相遇时,运动停止,设点P运动的路程为x,△BPQ的面积为y,则y关于x的函数图象大致是( )
A.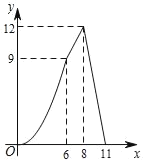 B.
B.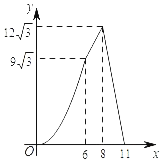
C.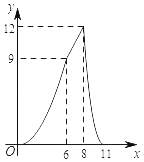 D.
D.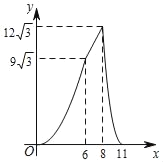
查看答案和解析>>
科目:初中数学 来源: 题型:
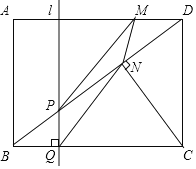
【题目】如图,在矩形ABCD中,CD=3cm,BC=4cm,连接BD,并过点C作CN⊥BD,垂足为N,直线l垂直BC,分别交BD、BC于点P、Q.直线l从AB出发,以每秒1cm的速度沿BC方向匀速运动到CD为止;点M沿线段DA以每秒1cm的速度由点D向点A匀速运动,到点A为止,直线1与点M同时出发,设运动时间为t秒(t>0).
(1)线段CN= ;
(2)连接PM和QN,当四边形MPQN为平行四边形时,求t的值;
(3)在整个运动过程中,当t为何值时△PMN的面积取得最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
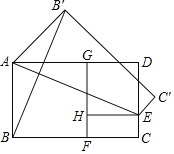
【题目】如图,在黄金矩形ABCD中,四边形ABFG、GHED均为正方形,![]() ,现将矩形ABCD沿AE向上翻折,得四边形AEC'B',连接BB',若AB=2,则线段BB'的长度为( )
,现将矩形ABCD沿AE向上翻折,得四边形AEC'B',连接BB',若AB=2,则线段BB'的长度为( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蛋黄酥是现下糕点界的网红,每一颗蛋黄酥金黄诱人的酥皮下都包着一颗细腻绵沙的咸蛋黄,其口口酥心,层层松软的特点让人难忘.某商家推出两款八粒装的蛋黄酥,其中麻薯豆沙蛋黄酥50元每盒,莲蓉千层蛋黄酥48元每盒,两款蛋黄酥非常畅销,平均每周销售额为344000元.
(1)受生产能力限制,该商家平时每周生产7000盒八粒装蛋黄酥,为了保证周销售额不变,则每周平均需生产麻薯豆沙蛋黄酥多少盒?
(2)在(1)的条件下,为了迎接双十一大促,该商家提前扩大生产能力,并在双十一当天,开展蛋黄酥促销活动,麻薯豆沙蛋黄酥售价降低了![]() a元,其销量在当天比平时周销量增加了2000盒,最后当天两款蛋黄酥的总销售额比平时周销售额还多96000元,求a的值.
a元,其销量在当天比平时周销量增加了2000盒,最后当天两款蛋黄酥的总销售额比平时周销售额还多96000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第二十四届冬季奧林匹克运动会将于2022年2月4日至2月20日在北京举行,北京将成为历史上第一座既举办过夏奥会又举办过冬奥会的城市.某区举办了一次冬奥知识网上答题竞赛,甲、乙两校各有![]() 名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
名学生参加活动,为了解这两所学校的成绩情况,进行了抽样调查,过程如下,请补充完整.
[收集数据]
从甲、乙两校各随机抽取![]() 名学生,在这次竞赛中他们的成绩如下:
名学生,在这次竞赛中他们的成绩如下:
甲:![]()
![]()
乙:![]()
![]()
[整理、描述数据]按如下分数段整理、描述这两组样本数据:
学校 人数 成绩 |
|
|
|
甲 |
|
|
|
乙 |
|
|
|
(说明:优秀成绩为![]() ,良好成绩为
,良好成绩为![]() 合格成绩为
合格成绩为![]() .)
.)
[分析数据]两组样本数据的平均分、中位数、众数如下表所示:
学校 | 平均分 | 中位数 | 众数 |
甲 |
|
|
|
乙 |
|
|
|
其中![]() .
.
[得出结论]
(1)小明同学说:“这次竞赛我得了![]() 分,在我们学校排名属中游略偏上!”由表中数据可知小明是 _校的学生;(填“甲”或“乙”)
分,在我们学校排名属中游略偏上!”由表中数据可知小明是 _校的学生;(填“甲”或“乙”)
(2)张老师从乙校随机抽取--名学生的竞赛成绩,试估计这名学生的竞赛成绩为优秀的概率为_ ;
(3)根据以上数据推断一所你认为竞赛成绩较好的学校,并说明理由: ;
(至少从两个不同的角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,点
,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 重合),以
重合),以![]() 为腰作等腰直角
为腰作等腰直角![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)观察猜想
如图1,当点![]() 在线段
在线段![]() 上时,
上时,
①![]() 与
与![]() 的位置关系为__________;
的位置关系为__________;
②![]() 之间的数量关系为___________(提示:可证
之间的数量关系为___________(提示:可证![]() )
)

(2)数学思考
如图2,当点![]() 在线段
在线段![]() 的延长线上时,(1)中的①、②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
的延长线上时,(1)中的①、②结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(3)拓展延伸
如图3,当点![]() 在线段
在线段![]() 的延长线时,将
的延长线时,将![]() 沿线段
沿线段![]() 翻折,使点
翻折,使点![]() 与点
与点![]() 重合,连接
重合,连接![]() ,若
,若![]() ,请直接写出线段
,请直接写出线段![]() 的长.(提示:做
的长.(提示:做![]() 于
于![]() ,做
,做![]() 于
于![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com