
ЁОЬтФПЁПЕАЛЦЫжЪЧЯжЯТИтЕуНчЕФЭјКьЃЌУПвЛПХЕАЛЦЫжН№ЛЦгеШЫЕФЫжЦЄЯТЖМАќзХвЛПХЯИФхУрЩГЕФЯЬЕАЛЦЃЌЦфПкПкЫжаФЃЌВуВуЫЩШэЕФЬиЕуШУШЫФбЭќЃЎФГЩЬМвЭЦГіСНПюАЫСЃзАЕФЕАЛЦЫжЃЌЦфжаТщЪэЖЙЩГЕАЛЦЫж50дЊУПКаЃЌСЋШиЧЇВуЕАЛЦЫж48дЊУПКаЃЌСНПюЕАЛЦЫжЗЧГЃГЉЯњЃЌЦНОљУПжмЯњЪлЖюЮЊ344000дЊЃЎ
ЃЈ1ЃЉЪмЩњВњФмСІЯожЦЃЌИУЩЬМвЦНЪБУПжмЩњВњ7000КаАЫСЃзАЕАЛЦЫжЃЌЮЊСЫБЃжЄжмЯњЪлЖюВЛБфЃЌдђУПжмЦНОљашЩњВњТщЪэЖЙЩГЕАЛЦЫжЖрЩйКаЃП
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЮЊСЫгНгЫЋЪЎвЛДѓДйЃЌИУЩЬМвЬсЧАРЉДѓЩњВњФмСІЃЌВЂдкЫЋЪЎвЛЕБЬьЃЌПЊеЙЕАЛЦЫжДйЯњЛюЖЏЃЌТщЪэЖЙЩГЕАЛЦЫжЪлМлНЕЕЭСЫ![]() aдЊЃЌЦфЯњСПдкЕБЬьБШЦНЪБжмЯњСПдіМгСЫ2000КаЃЌзюКѓЕБЬьСНПюЕАЛЦЫжЕФзмЯњЪлЖюБШЦНЪБжмЯњЪлЖюЛЙЖр96000дЊЃЌЧѓaЕФжЕЃЎ
aдЊЃЌЦфЯњСПдкЕБЬьБШЦНЪБжмЯњСПдіМгСЫ2000КаЃЌзюКѓЕБЬьСНПюЕАЛЦЫжЕФзмЯњЪлЖюБШЦНЪБжмЯњЪлЖюЛЙЖр96000дЊЃЌЧѓaЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉУПжмЦНОљашЩњВњТщЪэЖЙЩГЕАЛЦЫж4000КаЃЛЃЈ2ЃЉaЕФжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшУПжмЦНОљашЩњВњТщЪэЖЙЩГЕАЛЦЫжxКаЃЌдђУПжмЦНОљашЩњВњСЋШиЧЇВуЕАЛЦЫжЃЈ7000ЉxЃЉКаЃЌИљОнзмМлЃНЕЅМлЁСЪ§СПЃЌМДПЩЕУГіЙигкxЕФвЛдЊвЛДЮЗНГЬЃЌНтжЎМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉИљОнзмМлЃНЕЅМлЁСЪ§СПЃЌМДПЩЕУГіЙигкaЕФвЛдЊвЛДЮЗНГЬЃЌНтжЎМДПЩЕУГіНсТлЃЎ
НтЃКЃЈ1ЃЉЩшУПжмЦНОљашЩњВњТщЪэЖЙЩГЕАЛЦЫжxКаЃЌдђУПжмЦНОљашЩњВњСЋШиЧЇВуЕАЛЦЫжЃЈ7000ЉxЃЉКаЃЌ
вРЬтвтЃЌЕУЃК50x+48ЃЈ7000ЉxЃЉЃН344000ЃЌ
НтЕУЃКxЃН4000ЃЎ
Д№ЃКУПжмЦНОљашЩњВњТщЪэЖЙЩГЕАЛЦЫж4000КаЃЎ
ЃЈ2ЃЉвРЬтвтЃЌЕУЃКЃЈ50Љ![]() aЃЉЁСЃЈ4000+2000ЃЉ+48ЁСЃЈ7000Љ4000ЃЉЃН344000+96000ЃЌ
aЃЉЁСЃЈ4000+2000ЃЉ+48ЁСЃЈ7000Љ4000ЃЉЃН344000+96000ЃЌ
НтЕУЃКaЃН![]() ЃЎ
ЃЎ
Д№ЃКaЕФжЕЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
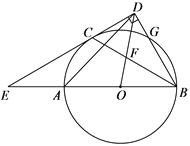
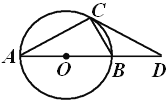
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌCЃЌGЪЧЁбOЩЯСНЕуЃЌЧв![]() ЃЌЙ§ЕуCЕФжБЯпCDЁЭBGгкЕуDЃЌНЛBAЕФбгГЄЯпгкЕуEЃЌСЌНгBCЃЌНЛODгкЕуFЃЎ
ЃЌЙ§ЕуCЕФжБЯпCDЁЭBGгкЕуDЃЌНЛBAЕФбгГЄЯпгкЕуEЃЌСЌНгBCЃЌНЛODгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКCDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓжЄЃКAE=AOЃЛ
ЃЌЧѓжЄЃКAE=AOЃЛ
ЃЈ3ЃЉСЌНг ADЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєCD ![]() ЃЌЧѓADЕФГЄЃЎ
ЃЌЧѓADЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
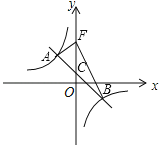
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§yЃНЉx+bЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН![]() (kЁй0)ЕФЭМЯѓНЛгкAЁЂBЕуЃЌгыyжсНЛгкЕуCЃЌЦфжаЕуAЕФАыБъЮЊ(Љ2ЃЌ3)
(kЁй0)ЕФЭМЯѓНЛгкAЁЂBЕуЃЌгыyжсНЛгкЕуCЃЌЦфжаЕуAЕФАыБъЮЊ(Љ2ЃЌ3)
(1)ЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
(2)ШчЭМЃЌШєНЋЕуCбиyжсЯђЩЯЦНвЦ4ИіЕЅЮЛГЄЖШжСЕуFЃЌСЌНгAFЁЂBFЃЌЧѓЁїABFЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЫЎВњЦЗбјжГЦѓвЕЮЊжИЕМИУЦѓвЕФГжжВњЦЗЕФбјжГКЭЯњЪлЃЌЖдРњФъЪаГЁааЧщКЭЫЎВњЦЗЕФбјжГЧщПіНјааСЫЕїВщЃЎЕїВщЗЂЯжетжжЫЎВњЦЗЕФУПЧЇПЫЪлМл![]() ЃЈдЊЃЉгыЯњЪлдТЗн
ЃЈдЊЃЉгыЯњЪлдТЗн![]() ЃЈдТЃЉТњзуЙиЯЕЪН
ЃЈдТЃЉТњзуЙиЯЕЪН![]() +36ЃЌЖјЦфУПЧЇПЫГЩБО
+36ЃЌЖјЦфУПЧЇПЫГЩБО![]() ЃЈдЊЃЉгыЯњЪлдТЗн
ЃЈдЊЃЉгыЯњЪлдТЗн![]() ЃЈдТЃЉТњзуЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃК
ЃЈдТЃЉТњзуЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃК
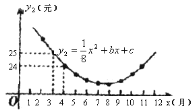
ЃЈ1ЃЉЪдШЗЖЈ![]() ЁЂ
ЁЂ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЧѓГіетжжЫЎВњЦЗУПЧЇПЫЕФРћШѓ![]() ЃЈдЊЃЉгыЯњЪлдТЗн
ЃЈдЊЃЉгыЯњЪлдТЗн![]() ЃЈдТЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈдТЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉМИдТЗнГіЪлетжжЫЎВњЦЗУПЧЇПЫРћШѓзюДѓ?зюДѓРћШѓЪЧЖрЩй?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАЫЋ11ЁБЕБЬьЃЌжиЧьЫГЗчПьЕнЙЋЫОГіЖЏЫљгаГЕСОЗжЩЯЮчЁЂЯТЮчСНХњЭљГЩЖМЫЭМўЃЌИУЙЋЫОЙВгаМзЁЂввЁЂБћШ§жжГЕаЭЃЌЦфжаМзаЭГЕЪ§СПеМЙЋЫОГЕСОзмЪ§ЕФ![]() ЃЌвваЭГЕСОЪЧБћаЭГЕЪ§СПЕФ2БЖЃЌЩЯЮчАВХХМзГЕЪ§СПЕФ
ЃЌвваЭГЕСОЪЧБћаЭГЕЪ§СПЕФ2БЖЃЌЩЯЮчАВХХМзГЕЪ§СПЕФ![]() ЃЌввГЕЪ§СПЕФ
ЃЌввГЕЪ§СПЕФ![]() ЃЌБћГЕЪ§СПЕФ
ЃЌБћГЕЪ§СПЕФ![]() НјаадЫЪфЃЌЧвЩЯЮчМзЁЂввЁЂБћШ§жжГЕаЭУПСОдиЛѕСПЗжБ№ЮЊ15ЖжЃЌ10ЖжЃЌ20ЖжЃЌдђЩЯЮчИеКУдЫЭъЕБЬьШЋВППьМўжиСПЕФ
НјаадЫЪфЃЌЧвЩЯЮчМзЁЂввЁЂБћШ§жжГЕаЭУПСОдиЛѕСПЗжБ№ЮЊ15ЖжЃЌ10ЖжЃЌ20ЖжЃЌдђЩЯЮчИеКУдЫЭъЕБЬьШЋВППьМўжиСПЕФ![]() ЃЛЯТЮчАВХХЪЃЯТЕФЫљгаГЕСОдЫЪфЭъЕБЬьЪЃЯТЕФЫљгаПьМўЃЌЧвЯТЮчМзЁЂввЁЂБћШ§жжГЕаЭУПСОдиЛѕСПЗжБ№ВЛЕУГЌЙ§20ЖжЃЌ12ЖжЃЌ16ЖжЃЌЯТЮчвваЭГЕЪЕМЪдиЛѕСПЮЊЯТЮчМзаЭГЕУПСОЪЕМЪдиЛѕСПЕФ
ЃЛЯТЮчАВХХЪЃЯТЕФЫљгаГЕСОдЫЪфЭъЕБЬьЪЃЯТЕФЫљгаПьМўЃЌЧвЯТЮчМзЁЂввЁЂБћШ§жжГЕаЭУПСОдиЛѕСПЗжБ№ВЛЕУГЌЙ§20ЖжЃЌ12ЖжЃЌ16ЖжЃЌЯТЮчвваЭГЕЪЕМЪдиЛѕСПЮЊЯТЮчМзаЭГЕУПСОЪЕМЪдиЛѕСПЕФ![]() ЃЎвбжЊЭЌжжЛѕГЕУПСОЕФЪЕМЪдиЛѕСПЯрЕШЃЌМзЁЂввЁЂБћШ§жжГЕаЭУПСОГЕЯТЮчЕФдЫЪфГЩБОЗжБ№ЮЊ50дЊ/ЖжЃЌ90дЊ/ЖжЃЌ60дЊ/ЖжЃЎдђЯТЮчдЫЪфЪБЃЌвЛСОМзжжГЕЁЂвЛСОввжжГЕЁЂвЛСОБћжжГЕзмЕФдЫЪфГЩБОзюЩйЮЊ_____дЊЃЎ
ЃЎвбжЊЭЌжжЛѕГЕУПСОЕФЪЕМЪдиЛѕСПЯрЕШЃЌМзЁЂввЁЂБћШ§жжГЕаЭУПСОГЕЯТЮчЕФдЫЪфГЩБОЗжБ№ЮЊ50дЊ/ЖжЃЌ90дЊ/ЖжЃЌ60дЊ/ЖжЃЎдђЯТЮчдЫЪфЪБЃЌвЛСОМзжжГЕЁЂвЛСОввжжГЕЁЂвЛСОБћжжГЕзмЕФдЫЪфГЩБОзюЩйЮЊ_____дЊЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкABCDжаЃЌAEЦНЗжЁЯBADНЛБпBCгкEЃЌDFЦНЗжЁЯADCНЛБпBCгкFЃЌШєAD=11ЃЌEF=5ЃЌдђAB=_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
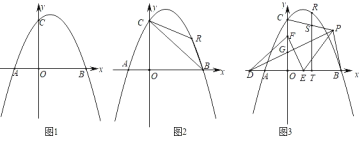
ЁОЬтФПЁПвбжЊЃКдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНax2Љ2ax+4ЃЈaЃМ0ЃЉНЛxжсгкЕуAЁЂBЃЌгыyжсНЛгкЕуCЃЌABЃН6ЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕуRЮЊЕквЛЯѓЯоЕФХзЮяЯпЩЯвЛЕуЃЌЗжБ№СЌНгRBЁЂRCЃЌЩшЁїRBCЕФУцЛ§ЮЊsЃЌЕуRЕФКсзјБъЮЊtЃЌЧѓsгыtЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШчЭМ3ЃЌЕуDдкxжсЕФИКАыжсЩЯЃЌЕуFдкyжсЕФе§АыжсЩЯЃЌЕуEЮЊOBЩЯвЛЕуЃЌЕуPЮЊЕквЛЯѓЯоФквЛЕуЃЌСЌНгPDЁЂEFЃЌPDНЛOCгкЕуGЃЌDGЃНEFЃЌPDЁЭEFЃЌСЌНгPEЃЌЁЯPEFЃН2ЁЯPDEЃЌСЌНгPBЁЂPCЃЌЙ§ЕуRзїRTЁЭOBгкЕуTЃЌНЛPCгкЕуSЃЌШєЕуPдкBTЕФДЙжБЦНЗжЯпЩЯЃЌOBЉTSЃН![]() ЃЌЧѓЕуRЕФзјБъЃЎ
ЃЌЧѓЕуRЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПеХРЯЪІдкНВНтИДЯАЁЖдВЁЗЕФФкШнЪБЃЌгУЭЖгАвЧЦСФЛеЙЪОГіШчЯТФкШнЃК
ШчЭМЃЌ![]() ФкНггк
ФкНггк![]() ЃЌжБОЖ
ЃЌжБОЖ![]() ЕФГЄЮЊ2ЃЌЙ§Еу
ЕФГЄЮЊ2ЃЌЙ§Еу![]() ЕФЧаЯпНЛ
ЕФЧаЯпНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЎ
ЃЎ
еХРЯЪІШУЭЌбЇУЧЬэМгЬѕМўКѓЃЌБржЦвЛЕРЬтФПЃЌВЂАДвЊЧѓЭъГЩЯТСаЬюПеЃЎ
ЃЈ1ЃЉдкЦСФЛФкШнжаЬэМгЬѕМў![]() ЃЌдђ
ЃЌдђ![]() ЕФГЄЮЊ______ЃЎ
ЕФГЄЮЊ______ЃЎ
ЃЈ2ЃЉвдЯТЪЧаЁУїЁЂаЁДЯЕФЖдЛАЃК
аЁУїЃКЮвМгЕФЬѕМўЪЧ![]() ЃЌОЭПЩвдЧѓГі
ЃЌОЭПЩвдЧѓГі![]() ЕФГЄ
ЕФГЄ
аЁДЯЃКФуетбљЬЋМђЕЅСЫЃЌЮвМгЕФЪЧ![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌОЭПЩвджЄУї
ЃЌОЭПЩвджЄУї![]() гы
гы![]() ШЋЕШЃЎ
ШЋЕШЃЎ
ВЮПМЩЯУцЖдЛАЃЌдкЦСФЛФкШнжаЬэМгЬѕМўЃЌБржЦвЛЕРЬтФПЃЈДЫЬтФПВЛНтД№ЃЌПЩвдЬэЯпЁЂЬэзжФИЃЉЃЎ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЦНааЫФБпаЮ![]() дкЦНУцжБНЧзјБъЯЕжаЃЌ
дкЦНУцжБНЧзјБъЯЕжаЃЌ![]() (Еу
(Еу![]() дкЕу
дкЕу![]() ЕФзѓВр)СНЕуЕФКсзјБъЪЧЗНГЬ
ЕФзѓВр)СНЕуЕФКсзјБъЪЧЗНГЬ![]() ЕФСНИіИљЃЌЕу
ЕФСНИіИљЃЌЕу![]() дк
дк![]() жсЩЯЃЌЦфжа
жсЩЯЃЌЦфжа![]() ЃЎ
ЃЎ
![]() Шє
Шє![]() ЪЧЕквЛЯѓЯоЮЛгкжБЯп
ЪЧЕквЛЯѓЯоЮЛгкжБЯп![]() ЩЯЗНЕФвЛЕуЃЌЙ§
ЩЯЗНЕФвЛЕуЃЌЙ§![]() зї
зї![]() гк
гк![]() Й§
Й§![]() зї
зї![]() жсгк
жсгк![]() ЕуЃЌзї
ЕуЃЌзї![]() жсНЛжБЯп
жсНЛжБЯп![]() гк
гк![]() ЮЊ
ЮЊ![]() жаЕуЃЌЦфжа
жаЕуЃЌЦфжа![]() ЕФжмГЄЪЧ
ЕФжмГЄЪЧ![]() ЃЛШє
ЃЛШє![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЖЏЕуЃЌ
ЩЯвЛЖЏЕуЃЌ![]() ЮЊжБЯп
ЮЊжБЯп![]() ЩЯвЛЖЏЕуЃЌСЌНг
ЩЯвЛЖЏЕуЃЌСЌНг![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕЃЌДЫЪБ
ЕФзюаЁжЕЃЌДЫЪБ![]() жсЩЯгавЛИіЖЏЕу
жсЩЯгавЛИіЖЏЕу![]() ЃЌЕБ
ЃЌЕБ![]() зюДѓЪБЃЌЧѓ
зюДѓЪБЃЌЧѓ![]() ЕузјБъЃЛ
ЕузјБъЃЛ
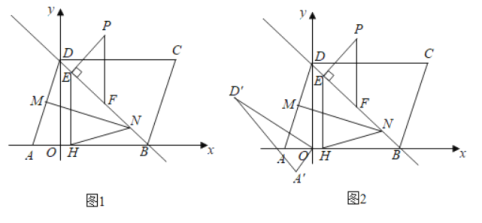
![]() дк
дк![]() ЕФЧщПіЯТЃЌНЋ
ЕФЧщПіЯТЃЌНЋ![]() ШЦ
ШЦ![]() ЕуФцЪБеыа§зЊ
ЕуФцЪБеыа§зЊ![]() КѓЕУЕН
КѓЕУЕН![]() ШчЭМ2ЃЌНЋЯпЖЮ
ШчЭМ2ЃЌНЋЯпЖЮ![]() бизХ
бизХ![]() жсЦНвЦМЧЦНвЦЙ§ГЬжаЕФЯпЖЮ
жсЦНвЦМЧЦНвЦЙ§ГЬжаЕФЯпЖЮ![]() ЮЊ
ЮЊ![]() ЃЌдкЦНУцжБНЧзјБъЯЕжаЪЧЗёДцдкЕу
ЃЌдкЦНУцжБНЧзјБъЯЕжаЪЧЗёДцдкЕу![]() ЃЌЪЙЕУвдЕу
ЃЌЪЙЕУвдЕу![]() ЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃЌШєДцдкЃЌЧыЧѓГіЕу
ЮЊЖЅЕуЕФЫФБпаЮЮЊСтаЮЃЌШєДцдкЃЌЧыЧѓГіЕу![]() ЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com