
【题目】如图,在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() 的坐标为
的坐标为![]() .平行于对角线
.平行于对角线![]() 的直线
的直线![]() 从原点
从原点![]() 出发,沿
出发,沿![]() 轴正方向以每秒1个单位长度的速度运动,设直线
轴正方向以每秒1个单位长度的速度运动,设直线![]() 与矩形
与矩形![]() 的两边分别交于点
的两边分别交于点![]() 、
、![]() ,直线
,直线![]() 运动的时间为
运动的时间为![]() (秒).
(秒).
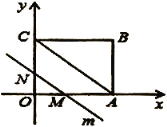
(1)点![]() 的坐标是_______,点
的坐标是_______,点![]() 的坐标是________;
的坐标是________;
(2)在![]() 中,当
中,当![]() 多少秒时,
多少秒时,![]() ;
;
(3)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式.
的函数关系式.
【答案】(1)(4,0),(0,3);(2)当t=2秒时,![]() ;(3)
;(3)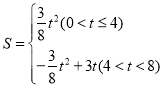 .
.
【解析】
(1)根据BC∥x轴,AB∥y轴即可求得A和C的坐标;
(2)判断出MN是△OAC的中位线进行讨论;
(3)求得AC的函数解析式,E的坐标是(t,0),则直线MN的解析式即可求得,则M和N的坐标即可求得,然后根据“S=矩形OABC的面积﹣Rt△OAM的面积﹣Rt△MBN的面积﹣Rt△NCO的面积”即可求得.
(1)A的坐标是(4,0),C的坐标是(0,3);
(2)∵MN∥AC,且![]() ,
,
∴MN是△OAC的中位线,
∵M是OA的中点,则![]() ;
;
(3)①当0<t≤4时,OM=t,
∵MN∥AC,
∴△OMN∽△OAC,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ;
;
②当4<t<8时,如图,
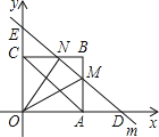
∵OD=t,
∴AD=t﹣4,
∵直线m∥AC,
∴∠MDA=∠CAO,
∴Rt△DAM∽Rt△AOC,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
同理得:△BMN∽△BAC,
∴![]() ,即
,即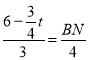 ,
,
∴![]() ,
,
∴CN=4-BN=t﹣4,
S=矩形OABC的面积﹣Rt△OAM的面积﹣Rt△MBN的面积﹣Rt△NCO的面积
![]() ;
;
∴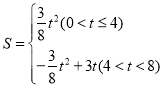 .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
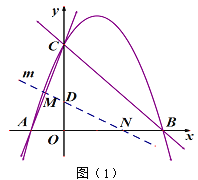
【题目】直线![]() 与x轴、y轴分别交于点B、C,抛物线
与x轴、y轴分别交于点B、C,抛物线![]() 经过点B、C,并与x轴交于另一点A.
经过点B、C,并与x轴交于另一点A.
(1)求此抛物线及直线AC的函数表达式;
(2)垂直于y轴的直线l与抛物线交于点P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),与直线BC交于点,N(
),与直线BC交于点,N(![]() ,
,![]() ),若
),若![]() <
<![]() <
<![]() ,结合函数的图象,求
,结合函数的图象,求![]() 的取值范围;
的取值范围;
(3)经过点D(0,1)的直线m与射线AC、射线OB分别交于点M、N.当直线m绕点D旋转时,![]() 是否为定值,若是,求出这个值,若不是,说明理由.
是否为定值,若是,求出这个值,若不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠疫情爆发后,各地启动了抗击新冠肺炎的一级应急响应机制,某社区20位90后积极参与社区志愿者工作,充分展示了新时代青年的责任担当,这20位志愿者的年龄统计如表,则他们年龄的众数和中位数分别是( )

A.25岁,25岁B.25岁,26岁C.26岁,25岁D.26岁,26岁
查看答案和解析>>
科目:初中数学 来源: 题型:
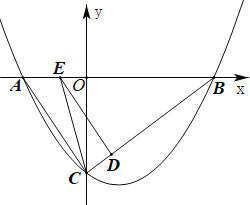
【题目】已知抛物线![]() 交x轴于A(-2,0),B(4,0)两点,交y轴于C点,连接AC、BC.点D在线段BC上(不与点B、点C重合),DE∥AC,交x轴于点E,连接CE.
交x轴于A(-2,0),B(4,0)两点,交y轴于C点,连接AC、BC.点D在线段BC上(不与点B、点C重合),DE∥AC,交x轴于点E,连接CE.
(1)求抛物线的解析式;
(2)设点D的横坐标为m,△CDE的面积为S.则m为何值时,S取得最大值,并求出这个最大值;
(3)若△ACE为等腰三角形,请直接写出此时点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学准备随机选出七、八、九三个年级各1名学生担任学校国旗升旗手.现已知这三个年级每个年级分别选送一男、一女共6名学生作为备选人.
(1)请你利用树状图或表格列出所有可能的选法;
(2)求选出“一男两女”三名国旗升旗手的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个函数,自变量x取a时,函数值y也等于a,我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2,且x1<1<x2,则c的取值范围是( )
A. c<﹣3B. c<﹣2C. c<![]() D. c<1
D. c<1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护环境卫生,垃圾分类开始实施.我市为了促进生活垃圾的分类处理,将生活垃圾分为“可回收物”、“有害垃圾”、“湿垃圾”、“干垃圾”四类,并且设置了相应的垃圾箱.

(1)小亮将妈妈分类好的某类垃圾随机投入到四种垃圾箱某类箱内,请写出小亮投放正确的概率为 ;
(2)经过妈妈的教育,小明已经分清了“有害垃圾”,但仍然分不清“可回收物”、“湿垃圾”和“干垃圾”,这天小亮要将妈妈分类好的四类垃圾投入到四种垃圾箱内,请求出小明投放正确的概率;
(3)请你就小亮投放垃圾的事件提出两条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图1,在![]() 中,
中,![]() ,点
,点![]() 是射线
是射线![]() 上任意一点,
上任意一点,![]() 是等边三角形,且点
是等边三角形,且点![]() 在
在![]() 的内部,连接
的内部,连接![]() .探究线段
.探究线段![]() 与
与![]() 之间的数量关系.
之间的数量关系.
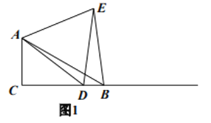
请你完成下列探究过程:
先将图形特殊化,得出猜想,再对一般情况进行分析并加以证明.
![]() 当点
当点![]() 与点
与点![]() 重合时(如图2),请你补全图形.由
重合时(如图2),请你补全图形.由![]() 的度数为_______________,点
的度数为_______________,点![]() 落在_______________,容易得出
落在_______________,容易得出![]() 与
与![]() 之间的数量关系为_______________
之间的数量关系为_______________
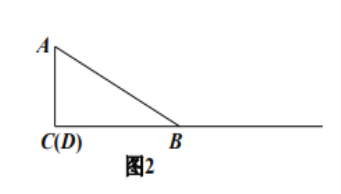
![]() 当
当![]() 是
是![]() 的平分线时,判断
的平分线时,判断![]() 与
与![]() 之间的数量关系并证明
之间的数量关系并证明
![]() 当点
当点![]() 在如图3的位置时,请你画出图形,研究
在如图3的位置时,请你画出图形,研究![]() 三点是否在以
三点是否在以![]() 为圆心的同一个圆上,写出你的猜想并加以证明.
为圆心的同一个圆上,写出你的猜想并加以证明.
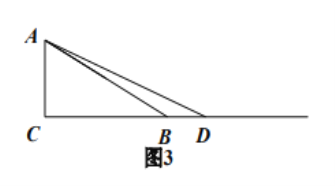
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com