
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ,
,![]() 相交于点
相交于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的值是_________;若
的值是_________;若![]() ,
,![]() ,则
,则![]() 的值是_________.
的值是_________.
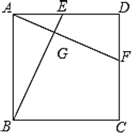
【答案】![]()
![]()
【解析】
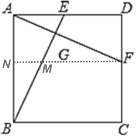
过F作FN∥AD交AB于N,交BE于M,利用平行线分线段成比例定理解答即可.
过F作FN∥AD交AB于N,交BE于M,
∵四边形ABCD是正方形,
∴AB∥CD,∵FN∥AD,
∴四边形ANFD是平行四边形,
∵∠D=90,
∴四边形ANFD是矩形,
若AE=ED,设AE=ED=a,则AD=DC=AB=NF=2a,
∵DF=FC,
∴AN=DF=BN=a,又MN∥AE,
∴BM=ME,
∴MN=![]() =
=![]() a,MF=NF-MN=
a,MF=NF-MN=![]() a,
a,
∵AE∥MF,
∴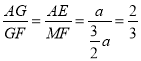 ;
;
若AE=3ED,设ED=m,则AE=3m,AD=AB=CD=FN=4m,AN=DF=2m,
同理证得:MN=![]() m,MF=
m,MF=![]() m,
m,
由AE//FM得: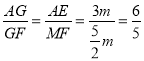 ,
,
故答案为:![]() ;
;![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B=45°,BC=4,BC边上的高AD=1,点P1、Q1、H1分别在边AD、AC、CD上,且四边形P1Q1H1D为正方形,点P2、Q2、H2分别在边Q1H1、CQ1、CH1上,且四边形P2Q2H2H1为正方形,…,按此规律操作下去,则线段CQ2020的长度为________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若一次函数y=ax+b和反比例函数y=-![]() 满足a+c=2b,则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.
满足a+c=2b,则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.
(1)判断y=x+b和y=-![]() 是否存在“等差”函数?若存在,写出它们的“等差”函数;
是否存在“等差”函数?若存在,写出它们的“等差”函数;
(2)若y=5x+b和y=-![]() 存在“等差”函数,且“等差”函数的图象与y=-
存在“等差”函数,且“等差”函数的图象与y=-![]() 的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;
的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;
(3)若一次函数y=ax+b和反比例函数y=-![]() (其中a>0,c>0,a=
(其中a>0,c>0,a=![]() b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1,y1)、B(x2,y2),试判断“等差”函数图象上是否存在一点P(x,y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.
b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1,y1)、B(x2,y2),试判断“等差”函数图象上是否存在一点P(x,y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
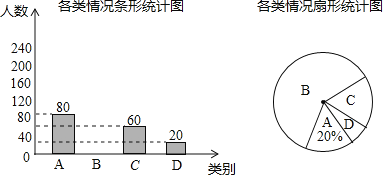
【题目】“安全教育”是学校必须开展的一项重要工作.某校为了了解家长和学生参与“暑期安全知识学习”的情况,进行了网上测试,并在本校学生中随机抽取部分学生进行调查.若把参与测试的情况分为![]() 类情形:
类情形:![]() .仅学生自己参与;
.仅学生自己参与;![]() .家长和学生一起参与;
.家长和学生一起参与;![]() .仅家长自己参与;
.仅家长自己参与;![]() .家长和学生都未参与.根据调查情况,绘制了以下不完整的统计图.请根据图中提供的信息,解答下列问题:
.家长和学生都未参与.根据调查情况,绘制了以下不完整的统计图.请根据图中提供的信息,解答下列问题:
![]() 在这次抽样调查中,共调查了 名学生;
在这次抽样调查中,共调查了 名学生;
![]() 补全条形统计图,并计算扇形统计图中
补全条形统计图,并计算扇形统计图中![]() 类所对应扇形的圆心角的度数;
类所对应扇形的圆心角的度数;
![]() 根据抽样调查结果,估计该校
根据抽样调查结果,估计该校![]() 名学生中“家长和学生都未参与”的人数.
名学生中“家长和学生都未参与”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(﹣3,y1),B(2,y2)均在抛物线y=ax2+bx+c上,点P(m,n)是该抛物线的顶点,若y1>y2≥n,则m的取值范围是( )
A.﹣3<m<2B.﹣![]() <m<-
<m<-![]() C.m>﹣
C.m>﹣![]() D.m>2
D.m>2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形,![]() 与
与![]() 恰好为对顶角,
恰好为对顶角,![]() ,连接
,连接![]() ,
,![]() ,点F是线段
,点F是线段![]() 上一点.
上一点.
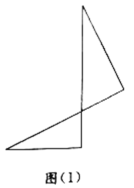
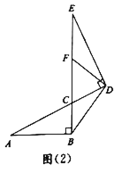
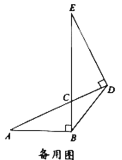
探究发现:
(1)当点F为线段![]() 的中点时,连接
的中点时,连接![]() (如图(2),小明经过探究,得到结论:
(如图(2),小明经过探究,得到结论:![]() .你认为此结论是否成立?_________.(填“是”或“否”)
.你认为此结论是否成立?_________.(填“是”或“否”)
拓展延伸:
(2)将(1)中的条件与结论互换,即:若![]() ,则点F为线段
,则点F为线段![]() 的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
问题解决:
(3)若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
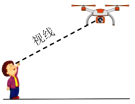
【题目】为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”.据测量,无人机与亮亮的水平距离是15米,当他抬头仰视无人机时,仰角恰好为![]() ,若亮亮身高1.70米,则无人机距离地面的高度约为________米.(结果精确到0.1米,参考数据:
,若亮亮身高1.70米,则无人机距离地面的高度约为________米.(结果精确到0.1米,参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在扇形![]() 中,圆心角
中,圆心角![]() ,半径
,半径![]() .
.
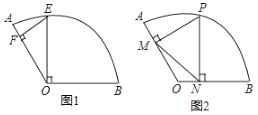
(1)如图1,过点![]() 作
作![]() ,交弧
,交弧![]() 于点
于点![]() ,再过点
,再过点![]() 作
作![]() 于点
于点![]() ,则
,则![]() 的长为_________,
的长为_________,![]() 的度数为_________;
的度数为_________;
(2)如图2,设点![]() 为弧
为弧![]() 上的动点,过点
上的动点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,点
,点![]() 分别在半径
分别在半径![]() ,
,![]() 上,连接
上,连接![]() ,则
,则
①求点![]() 运动的路径长是多少?
运动的路径长是多少?
②![]() 的长度是否是定值?如果是,请求出这个定值;若不是,请说明理由;
的长度是否是定值?如果是,请求出这个定值;若不是,请说明理由;
(3)在(2)中的条件下,若点![]() 是
是![]() 的外心,直接写出点
的外心,直接写出点![]() 运动的路经长.
运动的路经长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com