
【题目】如图,△ABC中,∠B=45°,BC=4,BC边上的高AD=1,点P1、Q1、H1分别在边AD、AC、CD上,且四边形P1Q1H1D为正方形,点P2、Q2、H2分别在边Q1H1、CQ1、CH1上,且四边形P2Q2H2H1为正方形,…,按此规律操作下去,则线段CQ2020的长度为________

【答案】![]()
【解析】
先求得BD、DC、AC的长,设P1D=x,则AP1=-x,P1Q1=H1Q1=H1D=P1D=x,再根据正方形性质可得AD//Q1H1,所以△ADC∽△CH1Q1,然后求的△ADC和△CH1Q1的相似比,同理求得△Q1H1C和△CH2Q2的相似比,然后总结规律即可解答.
解:∵BC边上的高AD=1,∠B=45°
∴BD=1
∴DC=BC-BD=4-1=3
∵AD⊥DC
∴AC=![]()
设P1D=x,则AP1=-x,P1Q1=H1Q1=H1D=P1D =x
∵P1Q1H1D是正方形
∴AD//Q1H1,
∴△ADC∽△CH1Q1,
∴![]() 即
即![]() ,解得x=
,解得x=![]()
∴P1Q1=H1Q1=H1D=P1D=![]() ,
,![]()
∴△ADC和△CH1Q1的相似比为![]()
同理:△Q1H1C和△CH2Q2的相似比![]()
∴△ADC和△CH2Q2的相似比![]()
依次类推,△ADC和△CH2020Q2020的相似比为![]()
∴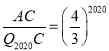 即
即
∴![]() =
=![]()
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】随着“微信运动”被越来越多的人关注和喜爱,某数学兴趣小组随机调查了我区50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | 0.16 |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | a |
12000≤x<16000 | b | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | 2 | 0.04 |
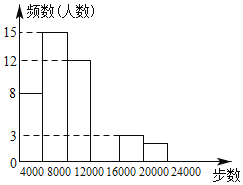
请根据以上信息,解答下列问题:
(1)写出a,b的值并补全频数分布直方图;
(2)我市约有5000名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步)的两名教师与大家分享心得,用树形图或列表法求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
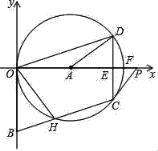
【题目】如图,⊙A过OBCD的三顶点O、D、C,边OB与⊙A相切于点O,边BC与⊙O相交于点H,射线OA交边CD于点E,交⊙A于点F,点P在射线OA上,且∠PCD=2∠DOF,以O为原点,OP所在的直线为x轴建立平面直角坐标系,点B的坐标为(0,﹣2).
(1)若∠BOH=30°,求点H的坐标;
(2)求证:直线PC是⊙A的切线;
(3)若OD=![]() ,求⊙A的半径.
,求⊙A的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
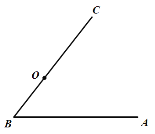
【题目】如图,点O在![]() 的边
的边![]() 上,以
上,以![]() 为半径作
为半径作![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于点D,过点D作
于点D,过点D作![]() 于点E.
于点E.
(1)尺规作图(不写作法,保留作图痕迹),补全图形;
(2)判断![]() 与
与![]() 交点的个数,并说明理由.
交点的个数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)求证:AM是⊙O的切线;
(2)若DC=2,求图中阴影部分的面积.(结果保留π和根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强环境保护意识,在“世界环境日”当天,在环保局工作人员指导下,若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组,随机抽查了全市40个噪声测量点在某时刻的噪声声级(单位:dB),并将抽查得到的数据进行整理(设所测数据是正整数),得频数分布表如下:
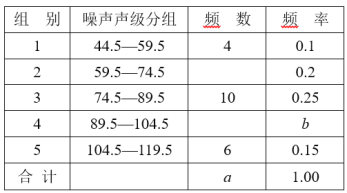

根据表中提供的信息解答下列问题:
(1)频数分布表中的a= ,b= ;
(2)补充完整频数分布直方图;
(3)这组数据的中位数落在第 小组内;
(4)如果全市共有400个测量点,那么在这一时刻噪声声级小于75dB的测量点约有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】贺岁片《流浪地球》被称为开启了中国科幻片的大门,2019也被称为中国科幻片的元年.某电影院为了全面了解观众对《流浪地球》的满意度情况,进行随机抽样调查,分为四个类别:A.非常满意;B.满意;C.基本满意;D.不满意.依据调查数据绘制成图1和图2的统计图(不完整).根据以上信息,解答下列问题:
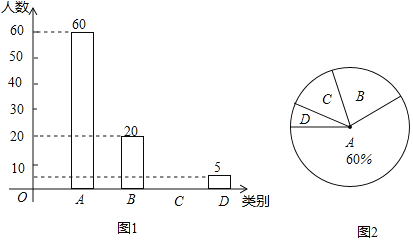
(1)本次接受调查的观众共有 人;
(2)扇形统计图中,扇形C的圆心角度数是 .
(3)请补全条形统计图;
(4)春节期间,该电影院来观看《流浪地球》的观众约3000人,请估计观众中对该电影满意(A、B、C类视为满意)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
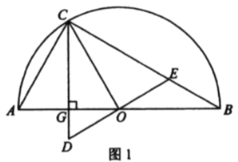
【题目】如图1,以![]() 为直径作半圆
为直径作半圆![]() ,点
,点![]() 在半圆上,连结
在半圆上,连结![]() 且
且![]() .连结
.连结![]() 是
是![]() 边上的高,过点
边上的高,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 于点
于点![]() .
.
![]() 求证:
求证:![]()
![]() 当
当![]() 为
为![]() 的中点时,求
的中点时,求![]() 的值.
的值.
![]() 如图2,取
如图2,取![]() 的中点
的中点![]() ,连结
,连结![]() .若
.若![]() 在点
在点![]() 运动过程中,当四边形
运动过程中,当四边形![]() 的其中一边长是
的其中一边长是![]() 的
的![]() 倍时,求所有满足条件的
倍时,求所有满足条件的![]() 长.
长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com