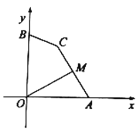
【题目】如图，点A，B的坐标分别为
，点C为坐标平面内一点，
，点M为线段
的中点，连接
，则的最大值为（ ）
A.
B.
C.
D.
名校联盟快乐课堂系列答案科目：初中数学 来源： 题型：
【题目】为了增强环境保护意识，在“世界环境日”当天，在环保局工作人员指导下，若干名“环保小卫士”组成的“控制噪声污染”课题学习研究小组，随机抽查了全市40个噪声测量点在某时刻的噪声声级（单位：dB），并将抽查得到的数据进行整理（设所测数据是正整数），得频数分布表如下：
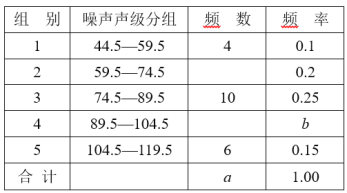
根据表中提供的信息解答下列问题：
（1）频数分布表中的a＝ ，b＝ ；
（2）补充完整频数分布直方图；
（3）这组数据的中位数落在第 小组内；
（4）如果全市共有400个测量点，那么在这一时刻噪声声级小于75dB的测量点约有多少个？
查看答案和解析>>
科目：初中数学 来源： 题型：
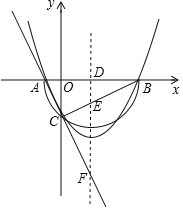
【题目】已知二次函数y＝x2+bx+c+1的图象与x轴交于点A（x1，0）、B（x2，0），且x1＜x2，与y轴的负半轴交于点C．
（1）当b＝1时，求c的取值范围；
（2）如果以AB为直径的半圆恰好过点C，求c的值；
（3）在（2）的条件下，如果二次函数的对称轴l与x轴、直线BC、直线AC的延长线分别交于点D、E、F，且满足DE＝2EF，求二次函数的表达式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】中国是最早发现并利用茶的国家，形成了具有独特魅力的茶文化2020年5月21日以“茶和世界共品共享”为主题的第一届国际茶日在中国召开．某茶店用4000元购进了A种茶叶若干盒，用8400元购进B种茶叶若干盒，所购B种茶叶比A种茶叶多10盒，且B种茶叶每盒进价是A种茶叶每盒进价的1.4倍．
（1）A，B两种茶叶每盒进价分别为多少元？
（2）第一次所购茶叶全部售完后第二次购进A，B两种茶叶共100盒（进价不变），A种茶叶的售价是每盒300元，B种茶叶的售价是每盒400元．两种茶叶各售出一半后，为庆祝国际茶日，两种茶叶均打七折销售，全部售出后，第二次所购茶叶的利润为5800元（不考虑其他因素），求本次购进A，B两种茶叶各多少盒？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
的函数解析式为
，若抛物线经过点
，对称轴为直线
．
（1）求抛物线的解析式．
（2）已知实数
，请证明：
，并说明
为何值时才会有
．
（3）若抛物线先向上平移4个单位，再向左平移1个单位后得到抛物线
，设
，
是上的两个不同点，且满足：
，
，
.请你用含有
的表达式表示出
的面积
，并求出的最小值及取最小值时一次函数
的函数解析式．
（参考公式：在平面直角坐标系中，若
，则
两点间的距离
）
查看答案和解析>>
科目：初中数学 来源： 题型：
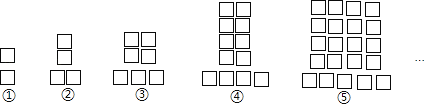
【题目】如图图形都是由同样大小的正方形“□”按照一定规律排列的，其中图①中共有2个正方形，图②中共有4个正方形，图③中共有7个正方形，图④中共有12个正方形，图⑤中共有21个正方形，……，照此规律排列下去，则图⑩中正方形的个数为_____．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
