
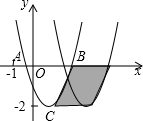
 如图,已知抛物线y=ax2+bx+c与轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论:
如图,已知抛物线y=ax2+bx+c与轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论:| A. | ①③ | B. | ②③ | C. | ②④ | D. | ③④ |
分析 ①首先根据抛物线开口向上,可得a>0;然后根据对称轴为x=-$\frac{b}{2a}$>0,可得b<0,据此判断即可.
②根据抛物线y=ax2+bx+c的图象,可得x=-1时,y>0,即a-b+c>0,据此判断即可.
③首先判断出阴影部分是一个平行四边形,然后根据平行四边形的面积=底×高,求出阴影部分的面积是多少即可.
④根据函数的最小值是$\frac{4ac-{b}^{2}}{4a}$,判断出c=-1时,a、b的关系即可.
解答 解:∵抛物线开口向上,
∴a>0,
又∵对称轴为x=-$\frac{b}{2a}$>0,
∴b<0,
∴结论①不正确;
∵x=-1时,y>0,
∴a-b+c>0,
∴结论②不正确;
∵抛物线向右平移了2个单位,
∴平行四边形的底是2,
∵函数y=ax2+bx+c的最小值是y=-2,
∴平行四边形的高是2,
∴阴影部分的面积是:2×2=4,
∴结论③正确;
∵$\frac{4ac-{b}^{2}}{4a}$=-2,c=-1,
∴b2=4a,
∴结论④正确.
综上,结论正确的是:③④.
故选D.
点评 此题主要考查了二次函数的图象与几何变换,二次函数的图象与系数的关系,熟练掌握平移的规律和二次函数的性质,解答此类问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种品牌童装 | 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 15 | 30 | 15 | |
| 乙种品牌童装 | 球 | 两红 | 一红一白 | 两白 |
| 礼金券(元) | 30 | 15 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 12 | C. | $\frac{1}{3}$ | D. | $\frac{1}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$+$\frac{1}{2}$=$\frac{2}{5}$ | B. | $\root{3}{-27}$=3 | C. | a10=(a5)2 | D. | b-2=-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com