
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′,A′C′交AB于点E.若AD=BE,则△A′DE的面积是 . 
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图![]() 的三边长分别为30,48,50,以它的三边中点为顶点组成第一个新三角形,再以第一个新三角形三边中点为顶点组成第二个新三角形,如此继续,则第6个新三角形的周长为______.
的三边长分别为30,48,50,以它的三边中点为顶点组成第一个新三角形,再以第一个新三角形三边中点为顶点组成第二个新三角形,如此继续,则第6个新三角形的周长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点![]() 点P第1次向上跳动1个单位至点
点P第1次向上跳动1个单位至点![]() ,紧接着第2次向左跳动2个单位至点
,紧接着第2次向左跳动2个单位至点![]() ,第3次向上跳动1个单位至点
,第3次向上跳动1个单位至点![]() ,第4次向右跳动3个单位至点
,第4次向右跳动3个单位至点![]() ,第5次又向上跳动1个单位至点
,第5次又向上跳动1个单位至点![]() ,第6次向左跳动4个单位至点
,第6次向左跳动4个单位至点![]() ,
,![]() 照此规律,点P第100次跳动至点
照此规律,点P第100次跳动至点![]() 的坐标是
的坐标是![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段AB=40cm.
(1)如图①,点P沿线段AB自点A向点B以3厘米/秒运动,同时点Q线段BA自B点向点A以5厘米/秒运动,问经过几秒后P、Q相遇?
(2)几秒钟后,P、Q相距16厘米?
(3)如图②,AO=PO=8厘米,∠POB=40°,点P绕点O以20度/秒的速度顺时针旋转一周停止,同时点Q沿直线BA自B点向点A运动,假若P、Q两点能相遇,求Q运动的速度.

查看答案和解析>>
科目:初中数学 来源: 题型:
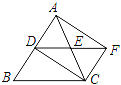
【题目】如图,在△BC中,AC=BC,点D、E分别是边AB、AC的中点.延长DE到点F,使DE=EF,得四边形ADCF.若使四边形ADCF是正方形,则应在△ABC中再添加一个条件为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在所给图形中:
⑴求证:∠BDC=∠A+∠B+∠C;
⑵如果点D与点A分别在线段BC的两侧,猜想∠BDC、∠A、∠B、∠C这4个角之间有怎样的关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值
(1)2x-{-3y+[3x-2(3x-y)]},其中x=-1,y=![]() .
.
(2)5(3a2b-ab2-1)-(ab2+3a2b-5),其中a=![]() ,b=
,b=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=6,点D是边BC的中点,点E是边AB上的任意一点(点E不与点B重合),沿DE翻折△DBE使点B落在点F处,连接AF,则线段AF的长取最小值时,BF的长为 . 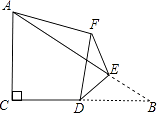
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com