
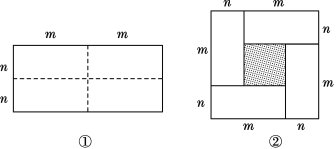
【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀把它均分成四个小长方形,然后按图②的形状拼成一个正方形.
(1)你认为图②中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图②中阴影部分的面积.
(3)观察图②你能写出下列三个代数式之间的等量关系吗?
代数式:(m+n)2,(m-n)2,mn.
(4)根据(3)题中的等量关系,解决如下问题:
已知a+b=7,ab=5,求(a-b)2的值.(写出过程)
【答案】解:(1)m-n;(2)详见解析;(3)(m+n)2=(m-n)2+4mn;(4)29.
【解析】
(1)观察可得阴影部分的正方形边长是m-n;
(2)方法1:边长为m+n的大正方形的面积减去4个长为m,宽为n的小长方形面积;
方法2:边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积;
(3)由(2)可得结论(m+n)2=(m-n)2+4mn;
(4)由(a-b)2=(a+b)2-4ab求解.
(1)阴影部分的正方形边长是m-n.
(2)阴影部分的面积就等于边长为m-n的小正方形的面积,
方法1:边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积,
即(m-n)2=(m+n)2-4mn;
方法2:边长为m+n的大正方形的面积减去长为2m,宽为2n的长方形面积,
即(m-n)2=(m+n)2-2m2n=(m+n)2-4mn;
(3)(m+n)2=(m-n)2+4mn.
(4)(a-b)2=(a+b)2-4ab=49-4×5=29.


科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+3与y轴交于A点,与反比例函数y= ![]() (x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0).
(x>0)的图象交于点B,过点B作BC⊥x轴于点C,且C点的坐标为(1,0). 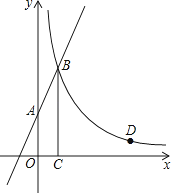
(1)求反比例函数的解析式;
(2)点D(a,1)是反比例函数y= ![]() (x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PB+PD最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知正方形的边长为4,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行,若乙的速度是甲的速度的3倍,则它们第2018次相遇在边 ( )上.
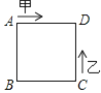
A. AB B. BC C. CD D. DA
查看答案和解析>>
科目:初中数学 来源: 题型:
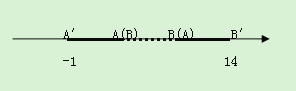
【题目】(1)如图,在数轴上有一小木棒AB,若平移木棒,使B落在A处,则A′所表示的数为 -1,若将A落在B处时,则B′所表示的数14,它的两个端点A、B所表示的数分别是 、 .
(2)老师给东东出了一道关于年龄的数学题:我像你那么小时,你才两岁;你像我那么大时,我已经44岁了,你猜我有多少岁?亲爱的同学,你能不能利用上一题的方法帮助小东求出老师的年龄呢?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com