
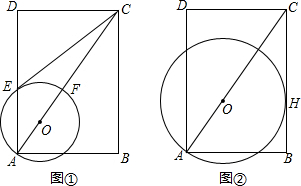
分析 (1)首先连接OE,由OE=OA与四边形ABCD是矩形,易求得∠DEC+∠OEA=90°,即OE⊥EC,即可证得直线CE与⊙O的位置关系是相切;
(2)根据等角的函数值相等,可得DE的长,根据线段的和差,可得AE的长,根据相似三角形的判定与性质,可得EF的长,AF的长,根据线段的和差,可得CF的长;
(3)根据相似三角形的判定与性质,可得关于r的方程,根据解方程,可得答案.
解答 (1)证明:如图1,连接OE.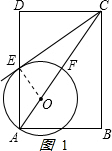 ,
,
∵四边形ABCD是矩形,
∴∠B=∠D=∠BAD=90°,BC∥AD,CD=AB.
∴∠DCE+∠DEC=90°,∠ACB=∠DAC.
又∵∠DCE=∠ACB,
∴∠DEC+∠DAC=90°,
∵OE=OA,
∴∠OEA=∠DAC,
∴∠DEC+∠OEA=90°,
∴∠OEC=90°,
∴OE⊥EC,)
∵OE为圆O半径,
∴直线CE与⊙O相切;
(2)如图2连接EF,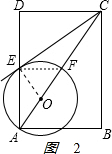 ,
,
由tan∠ACB=$\frac{\sqrt{3}}{2}$,BC=2,得
AB=$\sqrt{3}$.
由矩形的性质,得
DC=AB=$\sqrt{3}$,∠B=90°,
由勾股定理,得
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{2}^{2}}$=$\sqrt{7}$.
由∠ACB=∠DCE,得
tan∠DCE=$\frac{DE}{DC}$=tan∠ACB=$\frac{\sqrt{3}}{2}$,
DE=$\frac{\sqrt{3}}{2}$DC=$\frac{3}{2}$,
由线段的和差,得
AE=AD-DE=$\frac{1}{2}$.
由AF是⊙O的直径,得
∠AEF=90°,
EF∥DC,得
△AEF∽△ADC,
$\frac{EF}{DC}$=$\frac{AE}{AD}$,$\frac{AE}{AD}$=$\frac{AF}{AC}$,
EF=$\frac{AE}{AD}$•DC=$\sqrt{3}$×$\frac{\frac{1}{2}}{2}$=$\frac{\sqrt{3}}{4}$;
AF=AC•$\frac{AE}{AD}$=$\sqrt{7}$×$\frac{\frac{1}{2}}{2}$=$\frac{\sqrt{7}}{4}$,CF=AC-AF=$\sqrt{7}$-$\frac{\sqrt{7}}{4}$=$\frac{3\sqrt{7}}{4}$
C与圆上各点线段之间的最长距离是AC=$\sqrt{7}$,
C与圆上各点线段之间的最短距离是CF=$\frac{3\sqrt{7}}{4}$;
(3)如图3: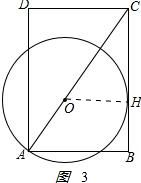
连接OH,设半径为r,
∵OH∥AB,
∴△OCH∽△OCB,$\frac{OH}{AB}$=$\frac{OC}{AC}$,即$\frac{r}{\sqrt{3}}$=$\frac{\sqrt{7}-r}{\sqrt{7}}$,
化简,得
($\sqrt{7}$+$\sqrt{3}$)r=$\sqrt{21}$,
解得r=$\frac{7\sqrt{3}-3\sqrt{7}}{4}$.
点评 本题考查了圆的综合题,(1)利用了矩形的性质,直角三角形的性质,余角的性质,切线的判定,利用余角的性质得出∠DEC+∠OEA=90°是解题关键;(2)利用了锐角三角函数,相似三角形的判定与性质;(3)利用相似三角形的性质得出关于r的方程是解题关键.


科目:初中数学 来源: 题型:解答题
 如图所示,以?ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.
如图所示,以?ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
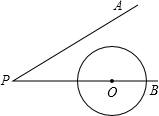 如图,∠APB=30°⊙O半径为1cm,圆心O在PB上,OP=3cm,若⊙O沿BP方向移动,当⊙O与直线PA相切时,圆心O移动的距离为1或5cm.
如图,∠APB=30°⊙O半径为1cm,圆心O在PB上,OP=3cm,若⊙O沿BP方向移动,当⊙O与直线PA相切时,圆心O移动的距离为1或5cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
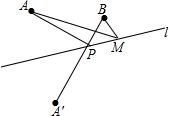 如图,已知A,B两点在直线1的同侧,点A′与A关于直线l对称,连接A′B交l于点P.若A′B=a.
如图,已知A,B两点在直线1的同侧,点A′与A关于直线l对称,连接A′B交l于点P.若A′B=a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-3,-2) | B. | (-2,-3) | C. | (2,3) | D. | (3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
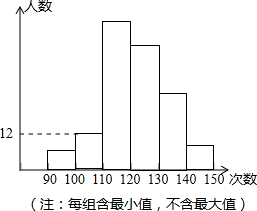 某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
某校为了了解九年级学生的体能情况,抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com