
【题目】如图,点![]() ,
,![]() 为定点,定直线
为定点,定直线![]() ,
,![]() 是
是![]() 上一动点,点
上一动点,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,对下列各值:
的中点,对下列各值:
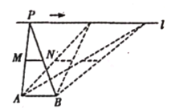
①线段![]() 的长;②
的长;②![]() 的面积;③
的面积;③![]() 的周长;④直线
的周长;④直线![]() ,
,![]() 之间的距离;⑤
之间的距离;⑤![]() 的大小,其中会随点
的大小,其中会随点![]() 的移动而变化的是( )
的移动而变化的是( )
A.②③B.②⑤C.③⑤D.④⑤
【答案】C
【解析】
根据三角形的中位线平行于第三边并且等于第三边的一半可得MN=![]() AB,从而判断①不变;确定点P到MN的距离不变,然后根据等底等高的三角形的面积确定出②不变;再根据三角形的周长的定义判断出③是变化的;根据平行线间的距离相等判断出④不变;根据角的定义判断出⑤变化.
AB,从而判断①不变;确定点P到MN的距离不变,然后根据等底等高的三角形的面积确定出②不变;再根据三角形的周长的定义判断出③是变化的;根据平行线间的距离相等判断出④不变;根据角的定义判断出⑤变化.
解:∵点A,B为顶点,M,N分别为PA,PB的中点,
∴MN是△PAB的中位线,
∴MN=![]() AB,即线段MN的长度不变,故①错误;
AB,即线段MN的长度不变,故①错误;
∵MN的长度不变,点P到MN的距离等于l与AB的距离的一半,
∴△PMN的面积不变,故②错误;
PA、PB的长度随点P的移动而变化,∴△PAB的周长会随点P的移动而变化,故③正确;
直线MN,AB之间的距离不随点P的移动而变化,故④错误;
∠APB的大小随点P的移动而改变,故⑤正确.
综合所述,会随点P的移动而变化的是③⑤.
故选C


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+2分别交x,y轴于点A、C,点P是该直线与反比例函数y=
x+2分别交x,y轴于点A、C,点P是该直线与反比例函数y=![]() 的图象,在第一象限内的交点,PB丄x轴,B为垂足,S△ABP=9.
的图象,在第一象限内的交点,PB丄x轴,B为垂足,S△ABP=9.
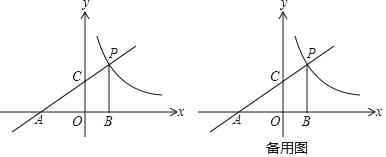
(1)直接写出点A的坐标_____;点C的坐标_____;点P的坐标_____;
(2)已知点Q在反比例函数y=![]() 的图象上,其横坐标为6,在x轴上确定一点M,使MP+MQ最小(保留作图痕迹),并求出点M的坐标;
的图象上,其横坐标为6,在x轴上确定一点M,使MP+MQ最小(保留作图痕迹),并求出点M的坐标;
(3)设点R在反比例函数y=![]() 的图象上,且在直线PB的右侧,做RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
的图象上,且在直线PB的右侧,做RT⊥x轴,T为垂足,当△BRT与△AOC相似时,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
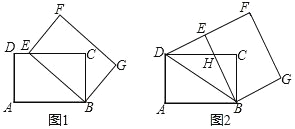
【题目】如图1,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.

(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形 ABCD 中,AB=5,AD=3.以点 B 为中心,顺时针旋转矩形 BADC,得到矩形 BEFG,点 A、D、C 的对应点分别为 E、F、G.
(1)如图1,当点 E 落在 CD 边上时,求线段 CE 的长;
(2)如图2,当点 E 落在线段 DF 上时,求证:∠ABD=∠EBD;
(3)在(2)的条件下,CD 与 BE 交于点 H,求线段 DH 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛![]() 的正南方向的
的正南方向的![]() 处,求还需航行的距离
处,求还需航行的距离![]() 的长.
的长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒子中装有形状、大小完全相同的3个小球,球上分别标有数字-1,1,2,从中随机取出一个,其上的数字记为k,放回后再取一次,其上的数记为b,则函数y=kx+b是增函数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.
(1)求证:∠CBP=∠ABP;
(2)若AB-BC=4,AC=8,求AE的长;
(3)当∠ABC=60°,BC=2时,点N为BC的中点,点M为边BP上一个动点,连接MC,MN,求MC+MN的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学兴趣小组在探究函数![]() 的图象和性质时,经历了以下探究过程:
的图象和性质时,经历了以下探究过程:
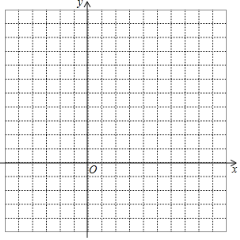
(1)列表如下:

写出表中m、n的值:m= ,n= ;
(2)描点并在图中画出函数的大致图象;
(3)根据函数图象,完成以下问题:
①观察函数![]() 的图象,以下说法正确的有 (填写正确的序号)
的图象,以下说法正确的有 (填写正确的序号)
A.对称轴是直线x=1;
B.函数![]() 的图象有两个最低点,其坐标分别是(﹣1,2)、(1,2);
的图象有两个最低点,其坐标分别是(﹣1,2)、(1,2);
C.当﹣1<x<1时,y随x的增大而增大;
D.当函数![]() 的图象向下平移3个单位时,图象与x轴有三个公共点;
的图象向下平移3个单位时,图象与x轴有三个公共点;
E.函数![]() 的图象,可以看作是函数
的图象,可以看作是函数![]() 的图象向右平移2个单位得到.
的图象向右平移2个单位得到.
②结合图象探究发现,当m满足 时,方程![]() 有四个解.
有四个解.
③设函数![]() 的图象与其对称轴相交于P点,当直线y=n和函数
的图象与其对称轴相交于P点,当直线y=n和函数![]() 图象只有两个交点时,且这两个交点与点P所构成的三角形是等腰直角三角形,则n的值为____________.
图象只有两个交点时,且这两个交点与点P所构成的三角形是等腰直角三角形,则n的值为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com