
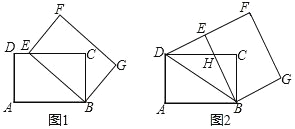
【题目】如图,在矩形 ABCD 中,AB=5,AD=3.以点 B 为中心,顺时针旋转矩形 BADC,得到矩形 BEFG,点 A、D、C 的对应点分别为 E、F、G.
(1)如图1,当点 E 落在 CD 边上时,求线段 CE 的长;
(2)如图2,当点 E 落在线段 DF 上时,求证:∠ABD=∠EBD;
(3)在(2)的条件下,CD 与 BE 交于点 H,求线段 DH 的长.
【答案】(1)4;(2)见解析;(3)DH= ![]() .
.
【解析】
(1)由旋转性质知BA=BE=5,由矩形性质知BC=AD=3,再在Rt△BCE中根据勾股定理可得;
(2)由旋转性质知∠BEF=∠A=90°,BE=BA,结合点E落在线段DF得∠BED=∠A=90°,再利用“HL”证△ABD≌△EBD即可得;
(3)设DH=x,从而得CH=5﹣x,再由矩形的性质知∠ABD=∠CDB,结合∠ABD=∠EBD知∠CDB=∠EBD,从而得DH=BH=x.在Rt△BCH中,根据CH2+BC2=BH2求解可得.
(1)由旋转的性质知BA=BE=5.
∵四边形ABCD是矩形,∴AD=BC=3,∠C=90°,∴CE![]() 4;
4;
(2)由旋转的性质知∠BEF=∠A=90°,BE=BA.
∵点E落在线段DF,∴∠BED=∠A=90°.
在△ABD和△EBD中,∵![]() ,∴△ABD≌△EBD(HL),∴∠ABD=∠EBD;
,∴△ABD≌△EBD(HL),∴∠ABD=∠EBD;
(3)设DH=x.
∵四边形ABCD是矩形,∴AB∥CD,AB=CD=5,∴CH=CD﹣DH=5﹣x,∠ABD=∠CDB.
又∵∠ABD=∠EBD,∴∠CDB=∠EBD,∴DH=BH=x.在Rt△BCH中,∵CH2+BC2=BH2,∴(5﹣x)2+32=x2,解得:x![]() ,∴DH
,∴DH![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题:
例:用图象法解一元二次不等式:![]() .
.
解:设![]() ,则
,则![]() 是
是![]() 的二次函数.
的二次函数.
![]() 抛物线开口向上.
抛物线开口向上.
又![]() 当
当![]() 时,
时,![]() ,解得
,解得![]() .
.
![]() 由此得抛物线
由此得抛物线![]() 的大致图象如图所示.
的大致图象如图所示.
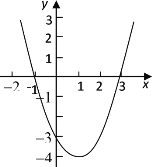
观察函数图象可知:当![]() 或
或![]() 时,
时,![]() .
.![]()
![]() 的解集是:
的解集是:![]() 或
或![]() .
.
(1)观察图象,直接写出一元二次不等式:![]() 的解集是 ;
的解集是 ;
(2)仿照上例,用图象法解一元二次不等式:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
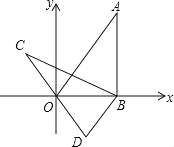
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为 .
x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,对于抛物线![]() ,下列说法中错误的是( )
,下列说法中错误的是( )
A.y的最小值为1
B.图象顶点坐标为(2,1),对称轴为直线x=2
C.当x<2时,y的值随x值的增大而增大,当x>2时,y的值随x值的增大而减小
D.它的图象可以由![]() 的图象向右平移2个单位长度,再向上平移1个单位长度得到
的图象向右平移2个单位长度,再向上平移1个单位长度得到
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
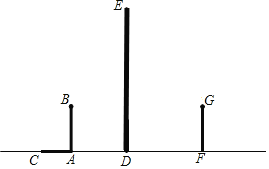
(1)请你确定灯泡所在的位置,并画出表示小亮在灯光下形成的影子线段.
(2)如果灯杆高12m,小亮的身高1.6m,小亮与灯杆的距离13m,请求出小亮影子的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,
,![]() 为定点,定直线
为定点,定直线![]() ,
,![]() 是
是![]() 上一动点,点
上一动点,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,对下列各值:
的中点,对下列各值:
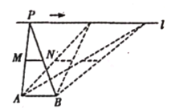
①线段![]() 的长;②
的长;②![]() 的面积;③
的面积;③![]() 的周长;④直线
的周长;④直线![]() ,
,![]() 之间的距离;⑤
之间的距离;⑤![]() 的大小,其中会随点
的大小,其中会随点![]() 的移动而变化的是( )
的移动而变化的是( )
A.②③B.②⑤C.③⑤D.④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90° ,AB=8,AC=10.点P以每秒1个单位长度的速度从A向B运动;同时点Q以每秒2个单位的速度从C向A运动.当其中一个点到达时,另一个点也随即停止运动,从出发开始___秒时,△APQ与△ABC相似.
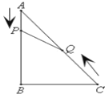
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为8的正方形纸片ABCD沿着EF折叠,使点C落在AB边的中点M处.点D落在点D'处,MD'与AD交于点G,则△AMG的内切圆半径的长为____________.
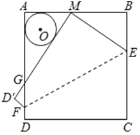
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com