
【题目】某数学兴趣小组在探究函数![]() 的图象和性质时,经历了以下探究过程:
的图象和性质时,经历了以下探究过程:
(1)列表如下:

写出表中m、n的值:m= ,n= ;
(2)描点并在图中画出函数的大致图象;
(3)根据函数图象,完成以下问题:
①观察函数![]() 的图象,以下说法正确的有 (填写正确的序号)
的图象,以下说法正确的有 (填写正确的序号)
A.对称轴是直线x=1;
B.函数![]() 的图象有两个最低点,其坐标分别是(﹣1,2)、(1,2);
的图象有两个最低点,其坐标分别是(﹣1,2)、(1,2);
C.当﹣1<x<1时,y随x的增大而增大;
D.当函数![]() 的图象向下平移3个单位时,图象与x轴有三个公共点;
的图象向下平移3个单位时,图象与x轴有三个公共点;
E.函数![]() 的图象,可以看作是函数
的图象,可以看作是函数![]() 的图象向右平移2个单位得到.
的图象向右平移2个单位得到.
②结合图象探究发现,当m满足 时,方程![]() 有四个解.
有四个解.
③设函数![]() 的图象与其对称轴相交于P点,当直线y=n和函数
的图象与其对称轴相交于P点,当直线y=n和函数![]() 图象只有两个交点时,且这两个交点与点P所构成的三角形是等腰直角三角形,则n的值为____________.
图象只有两个交点时,且这两个交点与点P所构成的三角形是等腰直角三角形,则n的值为____________.
【答案】(1)m=![]() ,n=
,n=![]() ;(2)见解析;(3)① B、D、E , ②2<m<3 , ③ 2或6
;(2)见解析;(3)① B、D、E , ②2<m<3 , ③ 2或6
【解析】
(1)把x=-![]() 和x=
和x=![]() 分别代入函数表达式,即可求得m,n;
分别代入函数表达式,即可求得m,n;
(2)按(1)的表格描点、连线即可;
(3)从函数图像上获取信息解答即可.
解:(1)把x=-![]() 和x=
和x=![]() 分别代入函数表达式,
分别代入函数表达式,
解得:y=![]() ,y=
,y=![]() :故答案为:
:故答案为:![]() ,
,![]() ;
;
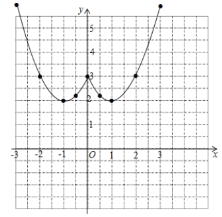
(2)如图所示
(3)
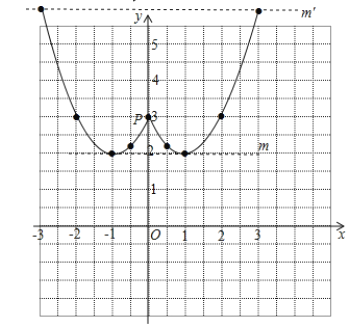
①A,如图:函数图像对称轴是直线x=0,故错误;
B.函数![]() 的图像有两个最低点,其坐标分别是(-1,2)、(1,2),故正确;C.当-1<x<1时,函数在y轴右侧,y随x的增大而减小,故错误;
的图像有两个最低点,其坐标分别是(-1,2)、(1,2),故正确;C.当-1<x<1时,函数在y轴右侧,y随x的增大而减小,故错误;
D.当函数![]() 的图像向下平移3个单位时,图像与x轴有三个公共点,正确;E.函数
的图像向下平移3个单位时,图像与x轴有三个公共点,正确;E.函数![]() 的图像,可以看作是函数
的图像,可以看作是函数![]() 的图像向右平移2个单位得到,正确;
的图像向右平移2个单位得到,正确;
故答案为:B,D、E;
②从图像看,2<m<3时,方程![]() 有四个解;
有四个解;
③如图,当直线y=n处于直线m或m1的位置时,点P和图像上的点构成等腰直角三角形,即n=2或6.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】阅读材料,解答问题:
例:用图象法解一元二次不等式:![]() .
.
解:设![]() ,则
,则![]() 是
是![]() 的二次函数.
的二次函数.
![]() 抛物线开口向上.
抛物线开口向上.
又![]() 当
当![]() 时,
时,![]() ,解得
,解得![]() .
.
![]() 由此得抛物线
由此得抛物线![]() 的大致图象如图所示.
的大致图象如图所示.
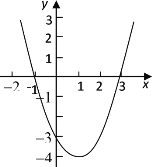
观察函数图象可知:当![]() 或
或![]() 时,
时,![]() .
.![]()
![]() 的解集是:
的解集是:![]() 或
或![]() .
.
(1)观察图象,直接写出一元二次不等式:![]() 的解集是 ;
的解集是 ;
(2)仿照上例,用图象法解一元二次不等式:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() ,
,![]() 为定点,定直线
为定点,定直线![]() ,
,![]() 是
是![]() 上一动点,点
上一动点,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,对下列各值:
的中点,对下列各值:
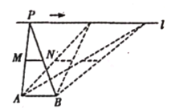
①线段![]() 的长;②
的长;②![]() 的面积;③
的面积;③![]() 的周长;④直线
的周长;④直线![]() ,
,![]() 之间的距离;⑤
之间的距离;⑤![]() 的大小,其中会随点
的大小,其中会随点![]() 的移动而变化的是( )
的移动而变化的是( )
A.②③B.②⑤C.③⑤D.④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
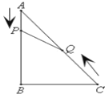
【题目】如图,在△ABC中,∠ABC=90° ,AB=8,AC=10.点P以每秒1个单位长度的速度从A向B运动;同时点Q以每秒2个单位的速度从C向A运动.当其中一个点到达时,另一个点也随即停止运动,从出发开始___秒时,△APQ与△ABC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹).
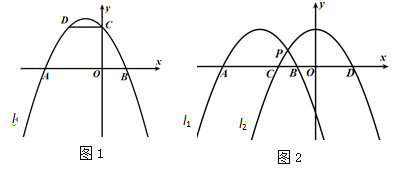
(1)如图1,抛物线l与x轴交于A,B两点,与y轴交于点C,CD∥x轴交抛物线于点D,作出抛物线的对称轴EF;
(2)如图2,抛物线l1,l2交于点P且关于直线MN对称,两抛物线分别交x轴于点A,B和点C,D,作出直线MN .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,![]() cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值 (单位:秒)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地特产槟榔芋深受欢迎,某商场以7元/千克收购了3000千克优质槟榔芋,若现在马上出售,每千克可获得利润3元.根据市场调查发现,近段时间内槟榔芋的售价每天上涨0.2元/千克,为了获得更大利润,商家决定先贮藏一段时间后再出售.根据以往经验,这批槟榔芋的贮藏时间不宜超过100天,在贮藏过程中平均每天损耗约10千克.
(1)若商家将这批槟榔芋贮藏x天后一次性出售,请完成下列表格:
每千克槟榔芋售价(单位:元) | 可供出售的槟榔芋重量(单位:千克) | |
现在出售 | 3000 | |
x天后出售 |
(2)将这批槟榔芋贮藏多少天后一次性出售最终可获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
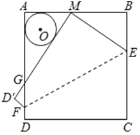
【题目】如图,将边长为8的正方形纸片ABCD沿着EF折叠,使点C落在AB边的中点M处.点D落在点D'处,MD'与AD交于点G,则△AMG的内切圆半径的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k为实数,关于x的方程为x2+(k+2)x+2k=1.
(1)判断方程有无实数根.
(2)当方程的根和k都是有理数时,请直接写出其中k的1个值和相应方程的根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com