
����Ŀ��ij���ز����������ܻ�ӭ��ij�̳���7Ԫ/ǧ���չ���3000ǧ���������������������ϳ��ۣ�ÿǧ�˿ɻ������3Ԫ�������г����鷢�֣�����ʱ������������ۼ�ÿ������0.2Ԫ/ǧ�ˣ�Ϊ�˻�ø��������̼Ҿ���������һ��ʱ����ٳ��ۣ������������飬���������������ʱ�䲻�˳���100�죬�����ع�����ƽ��ÿ�����Լ10ǧ�ˣ�
��1�����̼ҽ���������������x���һ���Գ��ۣ���������б���
ÿǧ���������ۼۣ���λ��Ԫ�� | �ɹ����۵���������������λ��ǧ�ˣ� | |
���ڳ��� | 3000 | |
x������ |
��2�����������������ض������һ���Գ������տɻ���������
���𰸡���1��10��![]() ��
��![]() ��2��39000Ԫ
��2��39000Ԫ
��������
(1)������֪����������ɣ�
(2)![]() �����ۣ����յ�����ϵ�������ۼ�
�����ۣ����յ�����ϵ�������ۼ�![]() ���������ɱ����г�������ϵʽ,��⼴��.
���������ɱ����г�������ϵʽ,��⼴��.
�⣺��1��7+3=10��Ԫ����
x�����۵��ۼ�Ϊ��10+0.2x��Ԫ/ǧ�ˣ�
�ɹ����۵�����������Ϊ��3000-10x��ǧ�ˣ�
�ʴ�Ϊ��10��![]() ��
��![]() ��
��
��2��������Ϊy��������ã�
![]()
=-2x![]() +500x+9000
+500x+9000
��-2<0,�������£��������ֵ
�Գ���x=![]()
�൱x<125ʱ��y��x�����������
�൱x=100ʱ��y���=-2��1002+500��100+9000=39000
�𣺽���������������100���һ���Գ������տɻ���������39000Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����һ�ž���ֽƬABCD���ŶԽ���BD�����۵�������C�䵽��E����BE��AD�ڵ�F.

(1)��֤����BDF�ǵ��������Σ�
(2)��ͼ2,����D��DG��BE����BC�ڵ�G������FG��BD�ڵ�O.
���ж��ı���BFDG����״����˵�����ɣ�
����AB=6��AD=8����FG�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90������PΪAC���ϵ�һ�㣬���߶�AP�Ƶ�A˳ʱ�뷽����ת����P��Ӧ��P��������AP��ת��AP����ABʱ����B��P��P��ǡ����ͬһֱ���ϣ���ʱ��P��E��AC�ڵ�E��
��1����֤����CBP=��ABP��
��2����AB-BC=4��AC=8����AE�ij���
��3������ABC=60����BC=2ʱ����NΪBC���е㣬��MΪ��BP��һ�����㣬����MC��MN����MC+MN����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ȤС����̽������![]() ��ͼ�������ʱ������������̽�����̣�
��ͼ�������ʱ������������̽�����̣�
��1���б����£�

д������m��n��ֵ��m�� ��n�� ��
��2����㲢��ͼ�л��������Ĵ���ͼ��
��3�����ݺ���ͼ������������⣺
�ٹ۲캯��![]() ��ͼ������˵����ȷ������ ������д��ȷ����ţ�
��ͼ������˵����ȷ������ ������д��ȷ����ţ�
A���Գ�����ֱ��x��1��
B������![]() ��ͼ����������͵㣬������ֱ��ǣ���1��2������1��2����
��ͼ����������͵㣬������ֱ��ǣ���1��2������1��2����
C������1��x��1ʱ��y��x�����������
D��������![]() ��ͼ������ƽ��3����λʱ��ͼ����x�������������㣻
��ͼ������ƽ��3����λʱ��ͼ����x�������������㣻
E������![]() ��ͼ���Կ����Ǻ���
��ͼ���Կ����Ǻ���![]() ��ͼ������ƽ��2����λ�õ���
��ͼ������ƽ��2����λ�õ���
�ڽ��ͼ��̽�����֣���m������ ��ʱ������![]() ���ĸ��⣮
���ĸ��⣮
���躯��![]() ��ͼ������Գ����ཻ��P�㣬��ֱ��y��n�ͺ���
��ͼ������Գ����ཻ��P�㣬��ֱ��y��n�ͺ���![]() ͼ��ֻ����������ʱ�����������������P�����ɵ��������ǵ���ֱ�������Σ���n��ֵΪ____________��
ͼ��ֻ����������ʱ�����������������P�����ɵ��������ǵ���ֱ�������Σ���n��ֵΪ____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
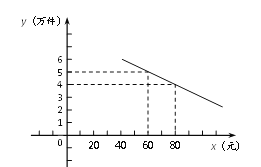
����Ŀ��ijͨѶ���Ĺ�˾����һ���г�����ϴ������ͨѶ��Ʒ����֪ÿ����Ʒ�Ľ���Ϊ40Ԫ��ÿ�����۸��ֲ�Ʒ���ܿ�֧���������ۣ�Ϊ120��Ԫ�������۹����з��֣���������![]() ������������۵���
������������۵���![]() ��Ԫ��֮���������ͼ��ʾ��һ�κ�����ϵ��
��Ԫ��֮���������ͼ��ʾ��һ�κ�����ϵ��
�� ֱ��д��![]() ����
����![]() �ĺ�����ϵʽΪ ��
�ĺ�����ϵʽΪ ��
�� �г��������Ź涨���ò�Ʒ���۵��۲��ó���100Ԫ���ù�˾���۸��ֲ�Ʒ�������55��Ԫ����������۵��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪��A��1��2����B��3��2��������AB��������ƽ����һ��P���߶�AB�϶����ڵ�Q��ʹ��PQ��2����Ƶ�P���߶�AB����Ӱ������
��1���ڵ�C��0��1����D��2��![]() ����E��4��5���У��߶�AB����Ӱ������ ��
����E��4��5���У��߶�AB����Ӱ������ ��
��2������M��m��n����ֱ��y=-x+2�ϣ��Ҳ����߶�AB����Ӱ��������m��ȡֵ��Χ��
��3����ֱ��y=![]() x+b�ϴ����߶�AB����Ӱ��������b��ȡֵ��Χ�Լ���Ӱ�������ɵ����������
x+b�ϴ����߶�AB����Ӱ��������b��ȡֵ��Χ�Լ���Ӱ�������ɵ����������
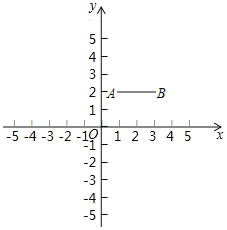
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
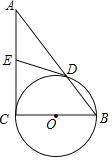
����Ŀ����ͼ������ABC�У���C=90������BCΪֱ���ġ�O��AB�ڵ�D����O������DE��AC�ڵ�E��
��1����֤��E��AC�е㣻
��2����AB=10��BC=6������CD��OE������ΪF����OF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�ؽ�ƽ����BD����ֱ�߷��ۣ�����Aǡ�����ڱ�BC���е�E����AE=BD����ôtan��ABD=��������
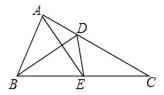
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCΪ��������Σ�AD��BC���ϵĸߣ�������EFGH��һ��FG��BC�ϣ�����E��H�ֱ���AB��AC�ϣ���֪BC��40cm��AD��30cm.
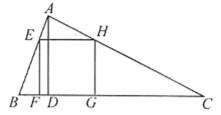
��1����֤����AEH�ס�ABC��
��2������������εı߳�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com